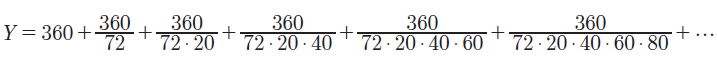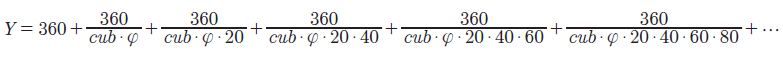Continuiamo con lo studio degli strumenti matematici necessari alla descrizione della Terra piatta. La matematica frattale è utile per descrivere il mondo naturale e la Terra.
L’idea è che la natura non può essere completamente spiegata con i numeri, che non possono cogliere l’essenza di ciò che viene descritto in quanto dobbiamo necessariamente tagliarli dopo qualche cifra decimale. Per comprendere meglio l’idea, è possibile stabilire una corrispondenza tra la geometria euclidea e quella frattale. Tutti conoscete la geometria euclidea, che può facilmente definire, con l’aiuto di coordinate e figure solide come un cubo o una sfera.
D’altra parte, molti problemi sorgono quando si desidera descrivere la forma di una nuvola. Probabilmente potremmo pensare che, teoricamente parlando, potrebbe essere una cosa fattibile ma, in pratica, è vero?
La cosa in realtà sarebbe difficile a causa del divario esistente tra la geometria euclidea e la natura. Rimanendo all’interno del campo euclideo puoi misurare perfettamente un segmento che va dal punto A al punto B. Ogni progettista Cad sa, ad esempio, che un segmento lungo 10 millimetri, disegnato al Cad, è esattamente 10 millimetri sul pc. Ma sa anche che il pezzo di acciaio che otterrà dall’officina, costruito secondo il suo disegno, non sarà esattamente di 10 millimetri, ma, forse, solo 9.97873457 … e misurerà con il suo calibro 9,98 perché quel calibro può misurare al massimo la centesima parte del millimetro (e solo nel caso abbia un calibro centesimale o un micrometro).
Si osservi l’immagine sotto riportata:
Proviamo a descrivere la forma di un cavolo romano con segmenti via via più corti. Per descrivere la forma di un oggetto, si può ottenere una precisione sempre maggiore utilizzando uno strumento di misura sempre più corto ma, tuttavia, non saremo mai in grado di avere una descrizione perfetta.
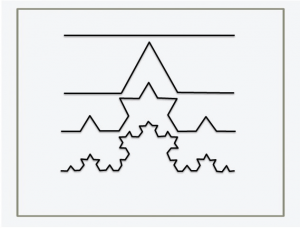
Si osservi la prima immagine dell’articolo: la curva triadica di Kock che illustra l’idea. Il primo passo è un segmento dritto. Il segmento viene quindi diviso in tre parti uguali. Quattro di queste parti vengono utilizzate per ottenere il secondo passo, che ormai è lungo L = 4/3. Questo processo può essere ripetuto all’infinito, senza alcuna limitazione. Qualsiasi segmento, indipendentemente dalla lunghezza, può sempre essere ulteriormente diviso. Questa è la geometria frattale.
La natura agisce in modo simile. Si ripete con strutture simili in scale sempre più piccole. Si può provare ad osservare la realtà nella scala più piccola possibile. Si può arrivare alla scala atomica. Quindi, a quelle dimensioni, sorgeranno problemi di diffrazione. Alla fine non saremo in grado di utilizzare alcuna fonte di luce per osservare, quindi, senza la tecnologia necessaria, dovremo fermarci. Forse, solo in futuro, saremo in grado di andare oltre grazie a nuove tecnologie.
Interessante è il fatto che anche il tempo si comporti in modo frattale. Vi siete mai chiesti perché i babilonesi e gli ebrei considerassero un anno fatto di 360 giorni? Consideravano l’ora come un cerchio, perché il loro orologio era il cielo e il cielo corre, durante l’anno, un cerchio di 360 °. Sono stati in grado di capire che c’era una differenza di circa un grado tra movimento del sole e delle stelle per ogni singolo giorno. Ciò significa che ogni giorno la stessa stella sorge 4 minuti prima, cioè un grado.
Hanno aggiunto i giorni rimanenti dell’anno con un mese intercalare in più. Questo modo di procedere è in accordo con la natura frattale del tempo.
Si consideri, ad esempio, l’anno siderale di 365,2564… giorni. Può essere espresso con frattali come questo: Y = 360 + 5 + 0,25 + 0,00625 + … Possiamo anche scrivere:
che può anche essere espresso in questo modo:
Si può dedurre, ovviamente, che il numero 72 ha una strana importanza nel definire la durata dell’anno. Mostrerò più avanti con un altro articolo, un altro fenomeno in cui è implicito il numero 72.
Il numero 72, incredibilmente, può essere espresso in questo modo:
72 = 44.4 × 1.62.
Incredibilmente perché? Perché 1,62 è un’approssimazione abbastanza buona di 1.618, cioè Phi o il numero aureo. Questo è il numero che di solito è stato associato alla descrizione frattale della natura. L’approssimazione è perché il phi è anch’esso irrazionale. Quindi possiamo scrivere: 72 = 44,4 x ϕ dove 44,4 è un numero con cifre ripetute. Mostrerò che questo è importante nella descrizione della Terra ed è collegato ai numeri di Fibonacci e Demlo. Per inciso, il cubito degli ebrei era di 44,4 centimetri.
Quindi se chiamiamo 44,4 cub (da cubit) la nostra Y può essere espressa in questo modo:
che è una incredibile descrizione frattale del tempo che ci permette di capire come mai gli Ebrei e i Babilonesi dicevano che un anno è di 360 giorni. Useremo metodi analoghi per descrivere molte delle misure della Terra.
Cercheremo sempre di trovare una descrizione frattale del fenomeno in osservazione. Trovare infatti la descrizione del corpo principale ci permetterà di conoscerne la natura intera. Basterà infatti ripetere i corpo principale in scala via via ridotta per avere la descrizione completa della realtà del fenomeno.
 Michele Vassallo è un ingegnere meccanico. Nel 2015, quando scoprì il movimento emergente degli American Flat Earthers, si sentì stupito e affascinato. Presto si rese conto che la Terra non poteva essere un globo. Nonostante il fatto che gli argomenti venuti alla ribalta fossero e siano ancora incompleti e contengano molti errori, il concetto generale di una terra piatta sembra assolutamente degno di indagine.
Michele Vassallo è un ingegnere meccanico. Nel 2015, quando scoprì il movimento emergente degli American Flat Earthers, si sentì stupito e affascinato. Presto si rese conto che la Terra non poteva essere un globo. Nonostante il fatto che gli argomenti venuti alla ribalta fossero e siano ancora incompleti e contengano molti errori, il concetto generale di una terra piatta sembra assolutamente degno di indagine.
Tra le sue migliori scoperte c’è la reintroduzione dell’etere nella fisica della terra piatta e una nuova visione della natura della luce.
E’ coautore del libro “The real measures of the (flat) Earth” edito da Aracne editore e del blog “rifugiatidipella.com“. Dal 2019 produce materiale video inerente la Terra piatta sul suo canale Youtube “earthmeasured”.