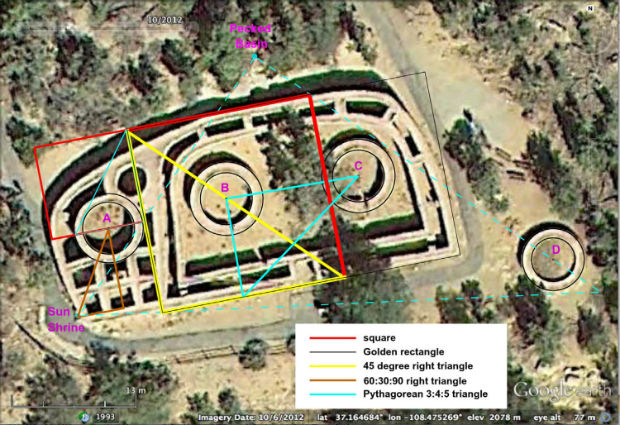
Modelli geometrici nascosti sono stati individuati nei primi templi eretti nell’America precolombiana. Gli antichi Pueblo non conoscevano la scrittura, eppure le sofisticate strutture contengono triangoli pitagorici e ‘rettangoli aurei’.
Centinaia di anni fa, l’antico popolo Pueblo, a sudovest dell’America precolombiana, è stato in grado di costruire strutture geometriche complesse con una precisione quasi perfetta. È stato
Tag: geometria sacra
I segreti dell’anima chiusi in un battistero
Il Battistero di Parma – e l’ho capito leggendo un libro assai speciale di Claudio Mutti, Il Linguaggio segreto dell’Antelami – non è un feticcio del turismo. È come un film – meglio, è come un romanzo – ma meglio ancora: è un’esperienza metafisica, un oltrepassare il mondo verso il cosmo, una vertigine sapienziale, un’immersione
Geometria Sacra: Intervista con Robert Lawlor
di Dorothea Rockburne e Christopher Bamford (da The Broolyn Rail)
Dopo un’assenza di molti anni, Robert Lawlor, che iniziò come scultore, e il cui libro Sacred Geometry ha avuto una grande influenza nel risvegliarci verso l’importanza di princìpi, simmetrie e proporzioni geometriche – non solo nell’arte e nell’architettura, ma anche negli studi scientifici e sulla
Anime della Distorsione – Cap5
La rinascita di un’antica scienza
Dall’altro estremo dello spettro scientifico nella scienza contemporanea, viene recuperata una antica scienza. Per ere è stata preservata con cura. E’ più o meno una forma d’arte ed è chiamata “geometria sacra”. Perchè sacra, cosa c’è di così sacro nella geometria? Nelle scuole misteriche spirituali del passato si insegnava che
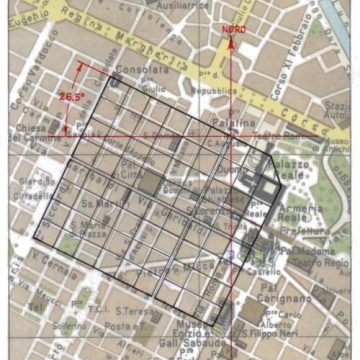
Torino e la Geometria Sacra
La probabile prova, che il mito di Osiri egizio, più che Fetonde greco, ha lasciato il segno matematico attraverso le diverse concezioni geometriche trattate in questo saggio.
David Wilcock: Il Cambio d’Era – cap. 5
– Argomentazioni Scientifiche dell’Ottava delle Dimensioni
In “Iperspazio” [1], il dott. Kaku descrive la vita di un intraprendente giovane matematico indiano conosciuto come Srinivasa Ramanujan. Le equazioni cui giunse Ramanujan sono ancora considerate le parti più importanti nella creazione del modello delle dimensioni superiori, incluso il numero di dimensioni che devono esistere. Se il modello