di Franco Maria Boschetto

Dopo aver stabilito questo nuovo sistema di unità di misura, possiamo inoltrarci nella parte più difficile della gravità quantistica.

Quando un effetto quantistico, come la produzione di particelle o l’energia del vuoto, influenza la curvatura dello spazio-tempo, la curvatura medesima diventa un oggetto quantistico, come il cono di luce visto sopra. Per lunghezze d’onda grandi rispetto alla lunghezza di Planck, le fluttuazioni quantistiche del campo gravitazionale quantizzato sono piccole, e possono essere trattate come una debole perturbazione dei risultati classici. Ma alle lunghezze d’onda e alle energie di Planck, la situazione si fa decisamente più complicata. Le particelle mediatrici del campo gravitazionale, i gravitoni da noi introdotti nel § 8.3, sono così debolmente interagenti con la materia ordinaria, che perfino un’intera galassia è quasi totalmente trasparente per essi. I gravitoni interagiscono apprezzabilmente con la materia solo quando raggiungono le energie di Planck; come si è visto, a tali energie essi si comportano né più e né meno come dei nanobuchi neri, e dunque sono in grado di indurre curvature significative nella geometria dello spazio, e di distorcerla completamente.

Da notare come l’energia trasportata da un gravitone sia in grado di distorcere non solo la geometria dello spazio tempo (cioè il tensore metrico), ma pure le onde associate al gravitone stesso. Questa è una conseguenza della non linearità della teoria di Einstein: quando si sovrappongono due campi gravitazionali, il campo risultante non è uguale alla somma dei due campi componenti. La teoria della gravità quantistica è perciò fortemente non lineare. Di solito si trattano le non linearità con un metodo di approssimazioni successive chiamato teoria delle perturbazioni, basata sul perfezionamento di un’approssimazione iniziale mediante una serie di correzioni progressivamente più piccole. Nel caso della gravità quantistica però la teoria delle perturbazioni non è applicabile perchè, ad una scala di energie paragonabili a quelle di Planck i successivi termini della serie di perturbazioni (cioè le successive correzioni) non sono affatto trascurabili, e troncare la serie a un numero finito di termini non porta a un’approssimazione valida, poiché nel quantizzare il campo gravitazionale si quantizza lo stesso spazio-tempo. Nell’ordinaria teoria quantistica dei campi lo spazio-tempo è un fondale di teatro fisso. Nella gravità quantistica il fondo non solo reagisce alle fluttuazioni quantistiche, ma fluttua esso stesso!

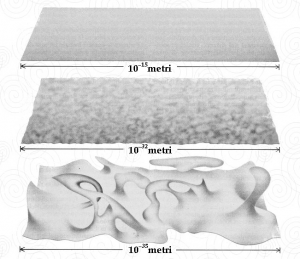
Osserviamo allo scopo lo schema sottostante. Il vuoto quantistico, cui si è accennato nel § 8.5, diventa sempre più caotico ispezionando regioni di spazio sempre più minuscole. Alla scala del nucleo atomico (la prima in alto), che è anche la più piccola cui riusciamo finora ad accedere con i nostri apparati sperimentali, lo spazio appare praticamente piatto. 17 ordini di grandezza più in basso (al centro) compaiono nella geometria delle irregolarità e delle asperità. Alla scala della lunghezza di Planck, 1000 volte più piccola ancora (in basso), la curvatura e la topologia dello spazio sono continuamente sottoposte a violente fluttuazioni, che trasformano la stessa tessitura dello spazio-tempo (si noti: non la materia e l’energia, bensì la stessa geometria) in un ribollire caotico ed imprevedibile, una sorta di “schiuma” che sfugge ad ogni tentativo di rappresentazione analitica.

Ma non è ancora finita. Uno spazio-tempo quantizzato possiede una struttura causale fluttuante e incerta anche per quanto riguarda il tempo. Alle dimensioni di Planck, difatti, la stessa distinzione passato e futuro diventa nebulosa. Per analogia con l’effetto tunnel nei sistemi quantistici, il quale consente a un elettrone di scavalcare una barriera energetica che potrebbe mai superare, dobbiamo aspettarci fenomeni non ammessi dalla tradizionale Relatività di Einstein, tra i qualiviaggi su distanze di Planck a velocità superiori a quella della luce. Non sappiamo ancora come calcolare le probabilità di tali fenomeni, proprio per via dell’assenza in una teoria gravitazionale quantistica coerente.

John Archibald Wheeler propose una descrizione di questo spazio-tempo distorto davvero intrigante, quella della cosiddetta topologia fluttuante. Se le fluttuazioni nel campo gravitazionale, come quelle di tutti i campi, aumentano di intensità mano a mano che ci si avvicina alle lunghezze d’onda di Planck, estrapolando a questa scala i risultati della Relatività Generale di Einstein (vedi § 7.8) si deduce che le fluttuazioni diventano talmente violente da provocare dei “buchi” nello spazio-tempo, analogamente ai “wormhole” tanto cari alla fantascienza. In altre parole, Wheeler immagina il vuoto quantistico in uno stato di perenne agitazione, con la continua comparsa e scomparsa di cunicoli (ma anche di strutture assai più complesse) di dimensioni paragonabili a quelle planckiane. La creazione di questi “cunicoli” è percepibile solo al livello di Planck; a scale dimensionali maggiori, lo spazio-tempo continua ad apparire più regolare che mai.

Se l’affascinante interpretazione di Wheeler è corretta, in quale misura le fluttuazioni topologiche contribuiscono all’energia del vuoto, e come influenzano la resistenza alla curvatura macroscopica dello spazio-tempo? Ma soprattutto, qual è la possibilità che questi benedetti cunicoli si aprano, collegando due punti diversi dello spazio-tempo “schiumoso”? Apparirebbe logico rispondere: un cunicolo topologico ha maggiori probabilità di congiungere due eventi tra loro”vicini”. Ma che cosa significa realmente “vicini”, in una metrica completamente distorta rispetto a quella cui siamo abituati? Si pensi al famoso “iperspazio”, introdotto nelle saghe di fantascienza di Isaac Asimov (il ciclo dei Robot e della Fondazione), in quella di “Star Wars” e in quella di “Babylon 5” per superare le distanze interstellari in alternativa al motore a curvatura di “Star Trek” e ai wormhole di “Stargate”. Esso non è forse tale da rendere vicini in esso due eventi che nello spazio-tempo ordinario appaiono lontanissimi?

Come si intuisce, la “vicinanza” non è una proprietà intrinseca della struttura spaziotemporale; anzi, in genere richiede l’esistenza di uno spazio con un maggior numero di dimensioni nel quale sia immerso lo spazio-tempo ordinario, cui siamo abituati, e questo spazio a più dimensioni deve essere dotato di proprietà metriche assai diverse da quelle del “nostro” universo. Ma allora… lo spazio-tempo non e più l’universo! L’universo è qualcosa di più. Tutto questo potrebbe seriamente danneggiare la dimensionalità macroscopica dello spazio. Se infatti i cunicoli si possono formare spontaneamente, gli stessi cunicoli possono formare altri cunicoli, e cosi via all’infinito. Lo spazio potrebbe evolvere quindi in una struttura che, sebbene tridimensionale alla scala di Planck, presenti invece quattro o più dimensioni in una scala maggiore. Basti pensare alla comune schiuma, che è costituita interamente da superfici bidimensionali (le bolle), ma dal punto di vista macroscopico ha una struttura tridimensionale.

8.9 Le dimensioni “arrotolate”

È però vero anche il viceversa: la dimensionalità apparente dello spazio-tempo potrebbe anche essere inferiore alla sua dimensionalità reale. Questa è stata storicamente proprio la prima soluzione proposta per cercare di inserire elettromagnetismo e gravità in un’unica teoria coerente dei campi. A proporla per primi furono il tedesco Theodor Kaluza (1885–1954) e lo svedese Oskar Klein (1894–1977). Inizialmente Albert Einstein sottovalutò il loro lavoro, ma in seguito l’autore della teoria della Relatività si convinse che la loro era la strada giusta per giungere alla Teoria di Grande Unificazione cui egli aspirava, e li incoraggiò a pubblicarne i risultati. Mentre nella Relatività Ristretta lo spazio è tridimensionale e lo spazio-tempo è tetradimensionale, nella Teoria di Kaluza-Klein lo spazio è tetradimensionale e lo spazio-tempo è pentadimensionale.

In pratica esiste una quarta dimensione spaziale, che noi non vediamo perchè è “arrotolata” lungo un cilindro con una circonferenza di diametro pari alla lunghezza di Planck (8.2), anziché essere “srotolata” come le altre tre lungo l’intera dimensione dell’universo, dell’ordine dei miliardi di anni luce. Nella Teoria di Kaluza-Klein, la traiettoria di tutte le particelle ha quindi una componente ciclica: ogni volta che raggiunge la massima estensione della dimensione arrotolata si ritrova al punto di partenza, e siccome questo continuo ruotare avviene lungo una scala spaziale miliardi di volte più piccola di un nucleo atomico, nessun esperimento a nostra disposizione può rivelarlo, e così noi non vediamo la quarta dimensione, ed abbiamo l’impressione che lo spazio sia tridimensionale.

Nonostante ciò, la quarta dimensione spaziale di Kaluza-Klein può manifestarsi in un altro modo, sotto forma di… luce. Kaluza e Klein infatti dimostrarono che se il loro spazio-tempo pentadimensionale viene trattato matematicamente allo stesso modo in cui lo spazio-tempo tetradimensionale viene trattato da Einstein, le componenti del campo elettromagnetico sono implicite nelle equazioni (7.10) in cui è coinvolta la curvatura dello spazio-tempo. Kaluza e Klein realizzarono in tal modo la prima valida teoria unificata dei campi, in grado di geometrizzare non solo la gravità, ma anche la radiazione elettromagnetica.

La Teoria di Kaluza-Klein conobbe un notevole successo negli anni venti, ma il suo problema era proprio la totale impossibilità di sottoporla a verifica sperimentale. Mentre la Gravitazione Universale di Newton si dimostrò in grado di prevedere correttamente l’esistenza e la posizione di Nettuno (§ 2.7), e la Relatività Generale riuscì a spiegare la deflessione della luce delle stelle (§ 6.8), la precessione del perielio di Mercurio (§ 6.9) e le lenti gravitazionali (§ 6.10), la teoria della quinta dimensione non prevedeva alcun nuovo fenomeno, e quindi non poteva essere confrontata con eventuali teorie alternative. La Teoria di Kaluza-Klein prevedeva effetti nuovi solo se venivano rimossi i limiti imposti dai suoi autori al modo in cui lo spazio-tempo può curvarsi nella dimensione aggiuntiva, ma nessuno di tali effetti trovò conferma sperimentale. La teoria venne quindi abbandonata, e riguardata al più come una intelligente curiosità matematica.

Se però ricordate quanto abbiamo detto nel § 7.9, già sapete che gli errori (o presunti tali) di una grande mente valgono più delle verità enunciate da una mente mediocre. Come la famosa costante cosmologica Λ di Einstein fu rispolverata allorché ci si avvide che l’universo sta accelerando e non rallentando, così anche la teoria di Kaluza-Klein venne riscoperta negli anni sessanta, quando si scopri che le nuove teorie di gauge che stavano destando un interesse crescente in vista della Grande Unificazione potevano essere riformulate proprio come teorie di Kaluza-Klein, nelle quali lo spazio è dotato non di una sola, ma di più dimensioni microscopiche aggiuntive, anch’esse “arrotolate” su una scala dimensionale pari a quella di Planck, e quindi invisibili ai nostri occhi, ed anche a quelli dei più potenti acceleratori di particelle. Si scoprì così che i due teorici degli anni venti avevano visto giusto, e che tutta la fisica si può tradurre in termini geometrici.

Dato che alla forza elettromagnetica e a quella gravitazionale si erano aggiunte la forza nucleare forte e la forza nucleare debole, una sola dimensione non è più sufficiente per descrivere le moderne teorie di gauge in termini di dimensioni “nascoste”. Tra tutte le versioni aggiornate dell’idea originaria di Kaluza e Klein formulate dagli scienziati, quella di maggior successo è la cosiddetta supergravità, ideata nel 1973 dal sovietico Dmitriy Volkov e poi perfezionata nel 1976 da Daniel Freedman, Peter van Nieuwenhuizen e Sergio Ferrara. Questa complicatissima teoria richiede che allo spazio-tempo di Einstein siano attribuite altre sette dimensioni oltre alle quattro ordinarie. Queste sette dimensioni non possono più essere arrotolate dentro un nanocilindro, ma vengono pensate come racchiuse dentro una struttura compatta chiamata eptasfera, una ipersfera a sette dimensioni. Ad ogni evento dello spazio-tempo ordinario di Einstein (x, y, z, t) è associata una eptasfera di dimensioni paragonabili alla scala di Planck, che contiene tutte le dimensioni “impacchettate”, dando alla geometria dell’universo il curioso aspetto raffigurato in questo disegno:

Una domanda sorge spontanea: perchè sono necessarie esattamente 11 dimensioni? Questo numero deriva da considerazioni matematiche inaspettate, che a prima vista nulla avrebbero a che fare con la gravità quantistica. Tutti gli studenti sono a conoscenza dell’esistenza dei numeri complessi, numeri del topo a + i b, formati da una parte reale a e da una parte immaginaria ottenuta moltiplicando un numero reale b per l’unità immaginaria i, ottenuta estraendo la radice di – 1 (si tratta di un numero che non appartiene al campo reale). Orbene, nel 1843 il matematico irlandese William Rowan Hamilton (1805-1865) scoprì che non è possibile realizzare dei numeri complessi con una parte reale e due unità immaginarie, del tipo a + i b + c j, ai quali possano essere estese le operazioni di moltiplicazione e divisione: un'”algebra di divisione” è ottenibile solo con quattro, otto, sedici, eccetera termini. I numeri complessi del tipo a + i b + c j + d k, con un’unità reale e tre immaginarie i, j, k sono detti quaternioni di Hamilton, ed oggi sono utilizzati in informatica per realizzare le rotazioni tridimensionali, e quindi sono usatissimi nei sistemi di controllo dei veicoli spaziali, ma anche nella progettazione di videogiochi. Per queste entità matematiche non vale più la proprietà commutativa del prodotto. I numeri complessi con un’unità reale e sette immaginarie sono detti invece ottetti di Cayley, dal nome del matematico inglese Arthur Cayley (1821–1895), e per essi il prodotto non è più nemmeno associativo.

Orbene, i fisici contemporanei hanno scoperto che le teorie supergravitazionali nelle quali non si consideri il tempo si possono formulare in modo coerente se tutte le particelle sono descritte proprio da ottetti di Cayley, e se la matematica che li descrive e l’algebra di divisione di questi esotici oggetti matematici. La supersimmetria emerge con naturalezza da questo tipo di descrizione, la normale moltiplicazione tra ottetti esprime le interazioni tra particelle, e tutte queste ultime, di qualsiasi tipo, usano lo stesso sistema numerico. Naturalmente il tempo non può essere trascurato; introducendolo, tuttavia, si modifica il numero di dimensioni, esattamente come un punto, privo di dimensioni, diventa una linea di dimensione uno, se viene rappresentato mentre si sposta nel tempo. Nella gravità quantistica l’introduzione del tempo aumentandolo di tre, non di uno, il numero di dimensioni. Se perciò uso gli ottetti per descrivere le particelle elementari statiche, quando ne studio l’evoluzione temporale ho bisogno di 11 dimensioni, non una di più, non una di meno. Con 12 o più dimensioni la supergravità fallisce nel tentativo di descrivere la realtà, e le sue equazioni non sono più valide. Se dunque la gravità quantistica è valida, gli ottetti di Cayley non sono più un inutile esercizio di stile matematico, ma forniscono la ragione profonda per cui il numero minimo di di dimensioni nascoste necessarie per includere tutte le quattro forze della natura in una sola descrizione matematica di tipo geometrico è proprio sette. Come dimostrano i casi dei numeri complessi o del calcolo differenziale assoluto di Gregorio Ricci Curbastro, non sarebbe certo la prima volta che un’invenzione puramente matematica fornisce gli esatti strumenti di cui hanno bisogno i fisici!

Naturalmente nelle dimensioni aggiuntive si prevedono fluttuazioni di curvatura, che si manifestano come particelle di grande massa. Si consideri infatti l’atomo quantistico: le configurazioni ondulatorie stazionarie corrispondono ad elettroni in moto lungo orbite percorse senza perdere energia. Allo stesso modo, le onde stazionarie sul “cilindro” della quinta dimensione di Kaluza e Klein corrispondono a particelle osservabili. Secondo la (8.5), la massa di ogni particella dipende dalla sua lunghezza d’onda, cioè dal rapporto tra la circonferenza del cilindro e il numero di oscillazioni che l’onda compie attorno ad essa: minore è la lunghezza d’onda, maggiore è l’energia dell’onda stessa, e più alta è la massa della particella ad essa associata. Le particelle di massa minore sono quelle associate a lunghezze d’onda grandissime. Tutte le configurazioni ondulatorie stazionarie consentite sul cerchio generano una serie di particelle le cui masse sono multipli interi della prima. E siccome la Teoria di Kaluza-Klein intendeva unificare gravitazione ed elettromagnetismo, tali particelle hanno anche una carica elettrica, inversamente proporzionale alla circonferenza. D’altra parte la carica di tutte le particelle da noi osservate è un multiplo intero di quella dell’elettrone, cosicché, se si ipotizza che questa sia la carica della prima particella pesante, se ne può calcolare anche la massa. La stessa cosa vale, mutatis mutandis, per le ipersfere della supergravità. I calcoli forniscono risultati curiosi: nella supergravità ogni particella fermionica (cioè a spin semintero, che segue la cosiddetta Statistica di Fermi-Dirac) ha un partner bosonico (a spin intero, che segue la Statistica di Bose-Einstein), e viceversa.

Tale particella viene detta anche superpartner, e la relazione tra ogni particella e il suo superpartner è detta supersimmetria (in inglese SUSY, da SUperSimmetrY). Lo spin del superpartner è sempre pari a quello della particella di partenza, diminuito di 1/2. Ne consegue che il gravitone, con spin 2, dovrebbe avere un superpartner chiamato gravitino, con spin 3/2. Il fotone, un bosone con spin 1, dovrebbe avere un superpartner fermionico con spin 1/2 chiamato fotino; l’elettrone, che è un fermione con spin 1/2, dovrebbe avere un superpartner con spin 0 chiamato selettrone, ed ogni quark con spin 1/2 dovrebbe essere accompagnato da un superbosone chiamato squark con spin nullo (il superpartner di un bosone ha per convenzione una denominazione che termina con -ino, mentre il superpartner di un fermione ne ha una che comincia con s-). Finora nessuna particella supersimmetrica è mai stata osservata in nessun esperimento, ma la loro scoperta potrebbe essere ardua, dato che le superparticelle possono avere masse fino a un migliaio di volte più grandi delle loro corrispondenti ordinarie. Il Large Hadron Collider del CERN di Ginevra potrebbe però essere in grado di generarne alcune; anche in questo caso, chi vivrà vedrà.

8.10 La musica dell’universo e il Big Splat

Negli anni ottanta ebbe successo una nuova teoria che prometteva di giungere alla Grande Unificazione: la Teoria delle Superstringhe. Si è detto sopra che, nelle teorie modellate su quella di Kaluza-Klein, le particelle possono essere associate alla quinta dimensione spaziale “arrotolata”. Infatti, secondo la Meccanica Quantistica, ogni particella può essere considerata anche come un’onda; per questo motivo, se qualche onda stazionaria è contenuta esattamente nella circonferenza del minuscolo “cerchio” avvolto lungo il nanocilindro o lungo le ipersfere, la corrispondente particella dovrebbe poter esistere nel comune spazio-tempo tetradimensionale. Ma allora, perchè non eliminare sfere e cilindri, e limitarsi a considerare la circonferenza vibrante, o anche solo una parte di essa? Nascono così nuove supposte entità fisiche, le superstringhe appunto: delle minuscole cordicelle monodimensionali che esistono in uno spazio multidimensionale. Ad ogni possibile modo vibrazionale di questi oggetti, corrispondono altrettante particelle. Questa teoria è estremamente affascinante, poiché ricorda da vicino un famosissimo brano del “Silmarillion”, la grande saga mitologica ideata dal sudafricano John Ronald Reuel Tolkien (1892–1973), nel quale si racconta che il mondo fu creato proprio da una canzone, l’Ainulindalë (“La Musica degli Ainur”), intonata dagli Ainur (“i Primi”, cioè gli déi) sotto la direzione di Ilúvatar, l’Essere Supremo:

« Nel principio Eru, l’Uno, che nella lingua elfica è detto Ilúvatar, creò gli Ainur dalla propria mente; e gli Ainur intonarono una Grande Musica al suo cospetto. In tale Musica, il mondo ebbe inizio, poiché Ilúvatar rese visibile il canto degli Ainur, e costoro lo videro quale una luce nell’oscurità. E molti di loro si innamorarono della sua bellezza e della sua vicenda che videro cominciare e svolgersi come in una visione. Per tale ragione Ilúvatar conferì Essere alla loro visione, e la collocò in mezzo al Vuoto, e il Fuoco Segreto fu inviato ad ardere nel cuore del Mondo; e questo fu chiamato Eä.»

La differenza principale tra la teoria delle superstringhe e quella della supergravità consiste nel modo in cui si deve contare il numero di particelle da esse previsto. Se le sette dimensioni in più della supergravità non fossero arrotolate entro un’ipersfera dell’ordine di grandezza della scala di Planck, la supergravità ad undici dimensioni prevederebbe un numero di particelle finito, mentre la compattazione in quello spazio ristretto dà vita ad un numero infinito di particelle: già la vecchia teoria pentadimensionale di Kaluza-Klein prevede una serie infinita di particelle perchè sono infinite le possibili configurazioni ondulatorie stazionarie lungo la quinta dimensione circolare. Invece, nella teoria delle supercorde si prevede un numero infinito di particelle anche senza compattazione delle dimensioni ulteriori, giacché esse corrispondono al numero infinito di configurazioni ondulatorie che possono avvenire sulle corde, esattamente come gli accordi degli Ainur secondo Tolkien diede vita all’infinità delle meraviglie dell’universo!

La maggior parte delle particelle prevista dalla teoria delle superstringhe ha una massa estremamente grande, più di 10^19 volte la massa del protone; essa però prevede anche circa 1000 particelle prive di massa. Inizialmente si pensava che le mutue interazioni tra queste particelle fossero equivalenti a quelle descritte da una versione della supergravità a 10 dimensioni, per la quale non esistono soluzioni alle equazioni nella quale sei dimensioni si arrotolano e lasciano uno spazio-tempo tetradimensionale con proprietà analoghe a quelle cui noi siamo abituati. In seguito, però, Michael Green (1946–) del Queen Mary College di Londra dimostrò che le interazioni delle particelle prive di massa previste dalla teoria delle superstringhe differiscono leggermente dalle loro interazioni nella versione della supergravità a 10 dimensioni: se si tiene conto degli effetti delle particelle pesanti, si ottengono equazioni coerenti a livello quantistico. Questo successo ha stimolato gli scienziati a percorrere la via delle superstringhe (la “Musica degli Ainur” della Fisica Moderna) per arrivare a una formulazione coerente della Grande Unificazione e della gravità quantistica, ma ben presto ci si accorse che la nuova via scelta offriva problemi di ancor più difficile soluzione che non nella supergravità ad undici dimensioni, dal momento che le proprietà delle superfici a sei dimensioni richieste nella teoria delle superstringhe sono matematicamente assai più complesse di quelle delle ipersfere a sette dimensioni. Ciononostante, le superstringhe hanno il vantaggio di spiegare a livello teorico l’esistenza dei gravitoni, il perché della presenza di certe particelle e non di altre, e perchè le particelle hanno proprio i valori osservati di spin, carica e massa. Per questo, molti scienziati continuano risoluti per questa strada, tanto che è stato detto che nessuno può fare carriera nel campo della Fisica delle Particelle, se per un po’ di tempo non ha lavorato sulle Superstringhe!

Tuttavia, il principale problema incontrato da questo approccio consiste nel fatto che nel corso degli ultimi anni sono state elaborate non una, ma ben cinque teorie coerenti delle superstringhe, che differiscono per il tipo di simmetrie implicate e per il tipo di vibrazioni permesse per le stringhe, il che vuol dire per il tipo di particelle previste. Cinque di esse prevedono la supersimmetria sopra vista, una invece prevede solo bosoni ma predice l’esistenza dei tachioni, particelle di massa a riposo immaginaria in grado di muoversi più veloci della luce, dei quali finora non si è giunti ad alcun riscontro sperimentale (i famosi neutrini più veloci della luce osservati dall’esperimento OPERA nei laboratori del Gran Sasso il 23 settembre 2011, che secondo alcuni sarebbero stati dei tachioni, si sono rivelati poi frutto di un errore di misurazione). La teoria supersimmetrica necessita non di undici, ma di ben ventisei dimensioni totali dello spazio-tempo! Come spesso avviene, però, quando una teoria diventa troppo complessa per risultare convincente (di solito la natura si basa su principi assai semplici), una nuova teoria arriva ad incasellare tutti i diversi risultati in un quadro più coerente. Nel nostro caso il matematico statunitense Edward Witten (1951–) nel 1995 dimostrò che le cinque suddette teorie delle superstringhe possono essere interpretate come cinque diverse formulazioni di una teoria ancora più basilare, la M-teoria. Questa va sotto il nome di Seconda Rivoluzione delle Superstringhe.

La M-teoria si basa su una generalizzazione del concetto di superstringa, la p-brana, dove p sta ad indicare il numero di dimensioni coinvolte. Di conseguenza la zero-brana è una particella puntiforme, la uno-brana coincide con una superstringa, la due-brana è una sorta di “membrana”; e così via: ogni p-brana ha una linea di universo in (p +1) dimensioni che si propaga attraverso lo spazio-tempo. Sviluppando i lavori di Witten, Joseph Polchinski (1954–) fece notare che, in certe situazioni, particolari tipi di superstringa non sarebbero in grado di muoversi in tutte le dimensioni a loro disposizione, e sarebbero incapaci di staccarsi da certe regioni dello spazio-tempo, sebbene assolutamente libere di muoversi in esse: Polchinski dimostrò che tali regioni erano proprio delle p-brane. Ma non tutte le superstringhe sono confinate all’interno delle brane: l’esistenza di stringhe chiuse riesce a spiegare anche l’estrema debolezza della gravità rispetto all’elettromagnetismo. Infatti la particella elementare responsabile della forza gravitazionale, il gravitone, corrispondendo ad una stringa chiusa, non è in alcun modo legato ad una brana, ed è per questo motivo che riesce a sfuggirle, facendo così sembrare meno intensa la forza di cui è responsabile! In seguito l’americano Andrew Strominger (1955–) e l’iraniano Cumrun Vafa 1960–) hanno dimostrato che la teoria delle p-brane può essere usata anche per conteggiare i microstati quantici associati alle diverse configurazioni dei buchi neri, e il risultato si è mostrato in buon accordo con le previsioni di Stephen Hawking. Il corrispettivo della teoria delle p-brane nelle approssimazioni a bassa energia sarebbe la già descritta teoria della supergravità.

In particolare, da tale teoria è possibile dedurre il cosiddetto principio olografico, proposto dall’olandese Gerardus ‘t Hooft (1946–) e dall’americano Leonard Susskind (1940–), secondo il quale è possibile descrivere ciò che avviene in un volume di spazio semplicemente usando una superficie. Il nome viene dall’analogia con i famosi ologrammi: per produrre un’immagine olografica si investe un oggetto tridimensionale con luce laser, la luce riflessa subisce interferenza con un raggio laser non perturbato, e la figura di interferenza viene registrata su una lastra fotografica. Colpendo quest’ultima con un raggio laser è possibile riprodurre la figura tridimensionale, pur partendo da uno schermo bidimensionale. Ebbene, ‘t Hooft e Susskind hanno dimostrato che la teoria delle p-brane presenta molte soluzioni di tipo olografico. Un esempio è costituito dalla cosiddetta corrispondenza AdS/CFT (acronimo di Anti de Sitter/Teoria di Campo Conforme): la teoria delle superstringhe in 10 dimensioni è equivalente a una teoria di campi di gauge in uno spazio di Minkowski a quattro dimensioni, il che vuol dire, in un linguaggio meno ermetico, che l’informazione contenuta nella teoria delle superstringhe in dieci dimensioni si può tradurre in una teoria di campo quadridimensionale e viceversa.

L’importanza di tutto ciò è enormemente maggiore dei paroloni dietro cui questa teoria si nasconde, poiché permette di interpretare il nostro universo quadridimensionale come immerso in un universo molto più ampio, a dieci dimensioni. Per descriverlo abbiamo due possibilità: o lo descriviamo come risultato delle oscillazioni delle superstringhe in dieci dimensioni, con tutta la complessità matematica del caso, oppure lo trattiamo come una teoria di campo a quattro dimensioni, a noi certamente più familiare. Ad esempio, la fisica delle particelle che cadono in un buco nero può essere registrata su uno schermo bidimensionale senza perdere informazione. I suoi sostenitori sperano che il principio olografico, applicato a problemi cosmologici tuttora aperti, ci possa svelare qualcosa di più sull’origine e sul destino del nostro universo.

Il principio olografico descrive un universo in cui l’energia oscura ha una densità negativa, deformando lo spazio-tempo in una cosiddetta geometria anti-de Sitter. In seguito Mikhail Vasiliev (1962–) e Efim Fradkin (1924–1999), fisici russi dell’Istituto Lebedev di Mosca, hanno ampliato il principio olografico applicandolo anche all’universo reale, nel quale l’energia oscura ha una densità positiva, con una geometria di de Sitter. Per riuscirci, hanno postulato un numero infinito di campi, descritte dalla proprietà dello spin, che può essere pensato come un grado di libertà rotazionale. La particella che fa da vettore al campo elettromagnetico, il fotone, ha spin – 1. Se lo si ruota di 360°, appare identico a se stesso. Il gravitone, vettore del campo gravitazionale, ha spin – 2: è necessario ruotarlo di soli 180° per farlo tornare uguale a se stesse. Le particelle di materia conosciute, come per esempio l’elettrone, hanno spin – 1/2: è necessario ruotarle di 720° prima di farle tornare al loro aspetto originario, una caratteristica assai poco intuitiva che riesce a spiegare perché queste particelle resistano al raggruppamento, dando alla materia la sua integrità.

Il famoso Bosone di Higgs ha spin 0 e sembra sempre lo stesso, comunque lo si ruoti. Ebbene, nella teoria di Vasiliev-Fradkin ci sono anche particelle con spin – 5/2, – 3, – 7/2, – 4, e così via. I fisici davano per scontato che ciò fosse impossibile, poiché questi campi di spin elevato, essendo più simmetrici, implicherebbero nuove leggi di natura analoghe alla conservazione di energia, e nessuna coppia di oggetti potrebbe mai interagire senza infrangere una di tali leggi. A prima vista, la teoria delle stringhe, principale candidato a diventare la teoria quantistica della gravitazione, si trova a dover fare i conti con questo principio. Come una corda di chitarra pizzicata, una stringa quantistica elementare ha un’infinità di armoniche superiori, che corrispondono a campi di spin più elevato. Ma queste armoniche hanno un costo energetico, che le rende inutilizzabili.

Ora, Vasiliev e Fradkin hanno dimostrato che questo ragionamento è valido solo quando la gravità è insignificante e lo spazio-tempo non è curvo. In uno spazio-tempo incurvato, i campi di spin elevato possono esistere. Supponiamo di avere un ipotetico spazio-tempo tridimensionale (due dimensioni spaziali, una temporale) saturo di particelle che interagiscono unicamente attraverso una versione potenziata della forza nucleare forte, in assenza della forza di gravità. In un simile contesto, gli oggetti di una certa grandezza possono interagire solo con oggetti di grandezza paragonabile, esattamente come gli oggetti che possono interagire solo se sono spazialmente adiacenti. La grandezza svolge esattamente lo stesso ruolo della posizione spaziale; si può pensare alla grandezza come a una nuova dimensione dello spazio, che si materializza dalle interazioni delle particelle come una figura di un libro pop-up.

L’originario spazio-tempo tridimensionale diventa il limite di uno spazio-tempo quadridimensionale, con la nuova dimensione che rappresenta la sua distanza da quel limite. Ma non emerge solo una dimensione spaziale, emerge anche la forza di gravità. Gli scienziati dicono che la forza nucleare forte nello spazio-tempo tridimensionale è il “duale” della gravità nello spazio-tempo quadridimensionale. Ora, la teoria di Vasiliev-Fradkin fa funzionare tutto questo anche in una geometria di de Sitter: il corrispondente limite tridimensionale è governato da un tipo di teoria del campo in cui il tempo non esiste, insomma in cui il campo è statico. La struttura di questa teoria dà luogo alla dimensione del tempo, che sorge in modo intrinsecamente asimmetrico, e questo spiegherebbe la “freccia del tempo”, cioè la sua unidirezionalità.

Secondo la teoria di Vasiliev-Fradkin, poi, i campi di spin elevato sono in possesso di un grado di simmetria ancora più elevato del campo gravitazionale, e maggiore simmetria significa meno struttura: anzi, troppo poca struttura per soddisfare anche le funzioni più elementari, come per esempio le relazioni di causa-effetto coerenti. Si dice che la teoria di Vasiliev-Fradkin è ancora meno lineare della Relatività Generale. Materia e geometria dello spazio-tempo sono così profondamente intrecciate che diventa impossibile considerarle separatamente, e la nostra familiare immagine della materia come residente nello spazio-tempo diventa completamente insostenibile. Nell’universo primordiale, dove regnava la teoria di Vasiliev-Fradkin, l’universo era un ammasso amorfo. Quando le simmetrie di spin più elevate si sono rotte (per esempio, quando le armoniche più alte delle stringhe quantistiche sono diventate troppo costose da mettere in moto), è emerso lo spazio-tempo nella sua interezza.

La M-teoria presuppone però un altro e ancor più incredibile sviluppo. Secondo i suoi autori, infatti, l’universo osservabile sarebbe formato solo da quattro delle undici dimensioni esistenti che si sono espanse al momento del Big Bang a differenza delle altre, rimaste arrotolate al modo di Kaluza-Klein; ma, soprattutto, il nostro universo sarebbe una 3-brana tridimensionale immersa in un iperspazio ad 11 dimensioni, realizzando una sorta di “profezia” dei telefilm di Babylon 5. La materia presente nell’Universo non può “uscire” da esso per entrare nell’iperspazio, poiché le superstringhe aperte tendono ad avere entrambe le estremità collegate ad una p-brana. Ma allora esisteranno altri universi paralleli, allocati in 3-brane adiacenti alla nostra: un’altra famosa predizione della fantascienza che si avvererebbe (basti pensare all’Universo dello Specchio nella saga di Star Trek, nel quale ogni personaggio del nostro cosmo ha una controparte cattiva) Negli universi paralleli o, se si preferisce, nelle 3-brane parallele potrebbero anche essere all’opera leggi fisiche diverse dalle nostre, come ipotizzato da Isaac Asimov nel suo romanzo “Neanche gli Déi” (1972); addirittura, potrebbe essere diverso il loro numero di dimensioni.

La loro presenza sarebbe evidenziata attraverso la reciproca attrazione gravitazionale. Ma l’americano Paul Steinhardt (1952–) e il sudafricano Neil Turok (1958–) si sono spinti ancora più in là, ipotizzando che il Big Bang sia stato originato da una collisione tra due brane che ha sviluppato sufficiente energia per dare vita al nostro universo: tale formidabile “scontro tra universi” è stato battezzato Big Splat. In teoria il Big Splat potrebbe essere dimostrato o meno da futuri e sensibilissimi sensori di onde gravitazionali, dal momento che, secondo il modello inflazionario (§ 7.6), le oscillazioni dell’inflatone avrebbero portato a distorsioni dello spazio-tempo e quindi ad onde gravitazionali percepibili, mentre nel modello delle p-brane il il Big Splat non originerebbe onde gravitazionali. L’estrema elusività delle onde di gravità rende però per il momento molto remota la speranza di una simile verifica sperimentale.

8.11 Lo spazio-tempo granulare e il Big Bounce

Prima di chiudere questo lungo capitolo dedicato ai tentativi di quantizzare la gravitazione, non possiamo fare a meno di discutere un’ulteriore teoria che ha conosciuto notevole successo negli ultimi anni, la cosiddetta Gravità Quantistica a Loop (LQG). Essa è stata ideata nel 1986 dal fisico indiano Abhay Ashtekar (1949–) della Pennsylvania State University, e poi rielaborata nel 1990 dall’italiano Carlo Rovelli (1956–) e dallo statunitense Lee Smolin (1955–). Questi ultimi si sono detti: per conciliare la teoria che spiega la gravitazione su larga scala, cioè la Relatività Generale, con la Meccanica Quantistica che disciplina il comportamento delle particelle suibatomiche, forse non c’è bisogno di quantizzare la gravità: basta quantizzare l’ambiente in cui essa opera. Infatti le equazioni su cui si basa la LQG conservano gli aspetti fondamentali della Relatività Generale, come ad esempio l’invarianza per trasformazioni di coordinate, ma portano le caratteristiche della meccanica quantistica alle loro estreme conseguenze, arrivando a quantizzare persino lo spazio e il tempo.

Non quindi la materia, l’energia o i campi: la stessa tessitura dello spazio-tempo alla scala di Planck. Lo spazio-tempo insomma, da continuo si trasforma in una sorta di rèticolo di dimensioni infinitesimali, come un muro composto da mattoni; in questo caso i mattoni sono il quanto spaziale, delle dimensioni della lunghezza di Planck (8.2), e il quanto temporale, dell’ordine del tempo di Planck (8.4). Spazio e tempo appaiono perciò come una sorta di “puzzle” fatto di tasselli piccolissimi, ed un cerchio non potrebbe assolutamente avere un contorno regolare, ma seguirebbe il profilo dei tasselli che lo compongono, apparendo un cerchio perfetto solo da lontano. Gli stessi tasselli infatti costituiscono ciò che noi chiamiamo “spazio” e “tempo”.

Ne consegue che, a livello della scala di Planck, il movimento avviene necessariamente a scatti, potendo ogni cosa avanzare nello spazio e nel tempo solo di un “quanto” per volta. I nostri sensi ci ingannano, facendoci percepire un flusso continuo perchè la lunghezza e il tempo di Planck sono al di là della capacità di risoluzione dei nostri sensi e del nostro cervello. In realtà però lo scorrere del tempo assomiglia piuttosto ad un film: i suoi fotogrammi si susseguono al ritmo di 24 al secondo, ma noi non ce ne accorgiamo e abbiamo l’illusione di un movimento continuo. « Il tempo non scorre come l’acqua di un fiume, ma come il ticchettio di un orologio », ha dichiarato Lee Smolin, il già citato coautore della teoria, « con rintocchi dell’ordine del tempo di Planck ».

Il punto di forza della Gravità Quantistica a Loop consiste nella semplicità con cui descrive fenomeni in cui la gravità è particolarmente intensa, e la struttura discreta diventa dominante. Le equazioni differenziali della Relatività Generale si trasformano infatti in Equazioni alle Differenze Finite, analoghe a quelle utilizzate nella Scienza delle Costruzioni per descrivere gli sforzi dentro muri e strutture edilizie, e risolubili per mezzo di supercomputer. I risultati emersi da queste equazioni sono sorprendenti: la gravità è da sempre considerata una forza attrattiva, ma le equazioni alle differenze finite suggeriscono invece che nelle condizioni di altissima densità ed energia che caratterizzano una singolarità, la gravità si trasformi in una forza repulsiva. L’esempio classico è quello di una spugna porosa (lo spazio-tempo) imbevuta di acqua (massa ed energia): essa può raccogliere fino ad una certa quantità di acqua ma, arrivata al limite, oltre a non raccoglierne più la respinge. Allora la singolarità del Big Bang aveva sì una densità elevatissima, tale da confinare nello spazio di un protone la massa di migliaia di galassie, ma essa era pur sempre una densità finita, mai infinita. Arrivati al limite di porosità energetica dello spazio, la gravità è divenuta repulsiva innescando il Big Bang e accelerando l’espansione dell’universo.

La conseguenza è incredibile. Il nostro universo potrebbe non essere partito da zero, ma derivare da un universo precedente collassato dalla gravità attrattiva che, arrivata alla soglia massima di energia dello spazio-tempo, si è trasformata in gravità repulsiva, espandendo lo spazio fino alle dimensioni attuali. Addirittura, se tutto ciò fosse vero, sarebbe possibile immaginare innumerevoli contrazioni e repulsioni, dovute all’alternarsi tra gravità attrattiva e gravità repulsiva, dando vita a un cosmo che continua a gonfiarsi, a ricontrarsi e a gonfiarsi di nuovo, come una palla che rimbalza sul pavimento! Per questo Smolin e collaboratori piuttosto che di Big Bang preferiscono parlare di Big Bounce (“grande rimbalzo”)!

La teoria ha un indubbio fascino, ma… come dimostrarla, se nessun microscopio ci può permettere di giungere a “vedere” gli atomi di spazio-tempo, né presumibilmente sarà mai possibile costruirne uno adeguato? Per via indiretta, ovviamente. Se lo spazio vuoto ha davvero una struttura granulare, esso si dovrebbe comportare, per certi aspetti, come un mezzo materiale, ad esempio per quel che riguarda la luce. Tutti sanno che la luce bianca entrata in un prisma si scompone nei diversi colori perchè l’indice di rifrazione dipende dalla frequenza: un fenomeno che è dovuto proprio alla struttura atomica del prisma. Secondo la Gravità Quantistica a Loop, qualcosa del genere dovrebbe accadere anche nel vuoto, ma non riguarderebbe la luce, bensì un’onda elettromagnetica con una frequenza assai maggiore e una lunghezza d’onda assai più piccola: i raggi gamma. Ora, il cosmo è spesso squassato da improvvise e violentissime esplosioni note come GRB (Gamma Ray Burst, esplosioni di raggi gamma), si pensa causate dalla collisione di due stelle a neutroni o di due buchi neri: se la teoria dello spazio-tempo quantizzato fosse vera, i raggi gamma con determinate frequenze raggiungerebbero i nostri strumenti un po’ prima di altri; in altre parole, la loro velocità potrebbe dipendere dalla loro energia.

I primi risultati sperimentali non sono molto incoraggianti. Il 10 maggio 2009 i sensori del Fermi Gamma-ray Space Telescope hanno analizzato i fotoni del GRB 090510, rivelando che, dopo una corsa durata 7,3 miliardi di anni, due fotoni gamma sono arrivati a tiro del sensore distanziati di appena nove decimi di secondo, nonostante uno dei due possedesse un milione di volte più energia dell’altro. Per quanto nella fisica delle particelle anche una discrepanza minima possa nascondere differenze molto significative, una differenza di nove decimi di secondo accumulata in un viaggio durato oltre sette miliardi di anni è talmente piccola da essere verosimilmente dovuta a specifici fenomeni avvenuti durante il processo di generazione del GRB, piuttosto cha alla granularità dello spazio-tempo. « Con uno scarto di una parte su 100 milioni di miliardi, i due fotoni hanno viaggiato alla stessa velocità: questa misurazione scarta le teorie sulla gravità che prevedono un cambiamento della velocità della luce in dipendenza dall’energia », ha dichiarato in modo perentorio Peter Michelson della Stanford University, che ha eseguito la suddetta misurazione. I sostenitori della Gravità Quantistica a Loop però non si arrendono, e sperano che future misurazioni forniscano piuttosto risultati in accordo con le loro previsioni.

Tra i partigiani del Big Bounce vi sono Roger Penrose (1931–) dell’Università di Oxford e Vahe Gurzadyan (1955–) dell’Università Statale di Yerevan, in Armenia. Essi hanno studiato per anni la radiazione cosmica di fondo di cui avviamo parlato nel § 7.4; come spiegano in un articolo sul sito arXiv, i due studiosi sostengono di aver scoperto la presenza di una serie di “cerchi concentrici” all’interno della radiazione di fondo, entro i quali la variazione di temperatura è molto inferiore al previsto; secondo i loro calcoli, alcuni dei cerchi più ampi potrebbero essersi formati prima del Big Bang, in seguito allo scontro di buchi neri supermassicci proprio al termine della contrazione dell’universo precedente al nostro. Alcuni però ritengono che questi “cerchi concentrici”, simili a quelli provocati da un sasso gettato nell’acqua, siano solo un’illusione dovuta agli strumenti utilizzati (i satelliti WMAP e BOOMERanG98), o che potrebbero comunque essere spiegati anche da altri modelli di universo.

Val la pena di citare anche il lavoro di Ivan Agullo e colleghi della Pennsylvania State University, i quali lavorano da molto tempo sulle condizioni dell’universo prima che si innescasse l’inflazione cosmica (la cosiddetta fase preinflazionaria): condizioni che, come abbiamo visto nei dettagli, necessitano giocoforza di una descrizione quantistica della gravità per poter essere individuate correttamente. Orbene, le fluttuazioni quantistiche all’origine delle attuali disomogeneità dell’universo si sono verificate entro un volume di Planck, ovvero in un cubo con lato pari alla lunghezza di Planck, e lo stato del vuoto in tale volume previsto dalla LQG differisce leggermente da quello della teoria classica dell’inflazione. Proprio questo aspetto dunque potrebbe rappresentare una “firma caratteristica” della Gravità Quantistica a Loop, che in un prossimo futuro potrebbe essere verificata sperimentalmente mediante le osservazioni cosmologiche, grazie a strumenti sempre più efficaci che gli scienziati stanno mettendo a punto.

8.12 L’universo frattale

Mi sembra corretto accennare ad altri tentativi di quantizzare la gravitazione. Uno dei programmi più importanti fu la cosiddetta Gravità Quantistica Euclidea, proposta dal famoso fisico Stephen Hawking. Il termine “euclideo” sta ad indicare che spazio e tempo sono trattati allo stesso identico modo. In pratica, l’universo non ha più tre dimensioni spaziali ed una temporale, ne ha quattro spaziali. È diventata celeberrima l’affermazione di Hawking: « Il tempo è una grandezza immaginaria », sia in senso matematico (l’unità immaginaria è la radice di – 1, una grandezza che non trova posto sulla retta reale) che nel senso posseduto da tale parola nel linguaggio corrente. Per gli abitanti di un simile universo, i concetti di “prima” e “dopo” non hanno senso, esattamente come accadeva in “Star Trek, Deep Space Nine” agli alieni che abitavano il tunnel spaziale bajoriano! Essi conoscevano il passato così come il futuro, perché le due realtà risultavano per loro coincidenti, ed è per questo che i Bajoriani li chiamavano “Profeti”.

Il metodo di Hawking si basa su un principio fondamentale della meccanica quantistica, il Principio di Sovrapposizione. Ogni oggetto, classico o quantistico, si trova in uno stato, ma mentre lo stato di un oggetto classico è caratterizzato da un unico e ben definito insieme di numeri, lo stato di un oggetto quantistico è assai più difficile da formalizzare, essendo dovuto alla sovrapposizione di tutti i possibili stati in cui il sistema si può trovare. Il moto di una palla da bowling o di un pianeta attorno al Sole è descritto da un’unica precisa traiettoria, mentre di un elettrone possiamo dire solo quale probabilità ha di seguire un certo itinerario piuttosto che un altro. Ne consegue che, quando un elettrone si muove da un punto all’altro, non si muove semplicemente lungo il segmento che congiunge i due punti, ma lungo tutti i possibili percorsi simultaneamente. La traiettoria “effettiva” dell’elettrone risulterà da una media ponderata di tutte le possibilità. Seguendo questo metodo, si può calcolare la probabilità di trovare l’elettrone in un qualsiasi intervallo di posizioni e di velocità. La Gravità Quantistica Euclidea applica il principio di sovrapposizione all’intero Universo: i diversi stati possibili su cui si esegue la media ponderata in questo caso sono tutti i diversi modi in cui l’universo potrebbe evolvere nel tempo e su larga scala, e quindi tutte le possibili geometrie dello spazio-tempo.

Dato che già lo studio delle varietà di Riemann appare difficilissimo, possiamo immaginare quanto lo sia sovrapporre tutte le varietà di Riemann possibili, ciascuna descritta da un complicatissimo Tensore di Ricci, Il metodo di Hawking è però diventato agevolmente applicabile dopo l’introduzione di potenti computer in grado di effettuare in un tempo relativamente breve una mole colossale di calcoli. A questo scopo, le geometrie riemanniane curve vengono sostituite con strutture approssimare composte da triangoli uniti l’un l’altro lungo i lati; tali triangoli vengono detti simplessi. Queste strutture composte da triangoli, simili per certi versi alle strutture realizzate con il gioco del geomag, possono essere trattate in modo agevole dai supercomputer; ovviamente le complesse strutture quadridimensionali dello spazio-tempo saranno realizzate con tetraedri tridimensionali, ma il principio non cambia.

Naturalmente i simplessi, triangolari o tetraedrici che siano, in realtà non esistono, trattandosi di una mera modellizzazione geometrica; attraverso di essi è però possibile studiarne il comportamento collettivo, tenendo conto che, se il loro numero tendesse all’infinito e le loro dimensioni a zero, staremmo descrivendo con precisione assoluta la varietà di Riemann in questione. L’indipendenza del comportamento globale da ciò che accade a piccola scala è detto « universalità », un concetto basilare nella Fisica Statistica.

Purtroppo, però, la Gravità Quantistica Euclidea non ha fornito risultati soddisfacenti: ben presto ci si è accorti infatti che gli universi costruiti con le simulazioni informatiche risultavano intrinsecamente instabili. Le fluttuazioni quantistiche su piccola scala della curvatura, caratteristica dei vari universi su cui si esegue la media ponderata, non si eliminavano affatto a vicenda per produrre l’universo classico, che è uniforme su larga scala; anzi, si sommavano rafforzandosi reciprocamente, facendo sì che l’universo si “accartocciasse” in una minuscola palla con un numero infinito di dimensioni, oppure desse vita a strane forme esotiche, certamente molto lontane dall’immagine che noi abbiamo del nostro cosmo.

Come uscire da questa impasse? Nel 1998 Jan Ambjørn del Niels Bohr Institute di Copenhagen, Jerzy Jurckiewicz dell’Università Jagellonica di Cracovia e Renate Loll dell’Università di Utrecht tentarono un approccio differente, da loro definito Triangolazione Dinamica Causale, partendo da uno dei punti deboli della teoria di Hawking e soci. La Gravità Quantistica Euclidea è difatti priva della nozione di causalità, perché non ha una nozione di tempo distinta dallo spazio, e quindi è impossibile disporre gli eventi in ordine cronologico. Hawking e collaboratori speravano che la causalità emergesse su larga scala a partire da fluttuazioni quantistiche microscopiche le quali, individualmente, non danno vita ad alcuna relazione causale. Le simulazioni al computer hanno però deluso questa speranza.

E così, invece di ignorare la causalità, Ambjørn, Jurckiewicz e Loll hanno deciso di incorporarla in uno stadio molto precedente. Ad ogni simplesso hanno assegnato una freccia del tempo dal passato al futuro, quindi hanno stabilito che due simplessi possano essere uniti tra loro solamente se le rispettive frecce del tempo puntano nella stessa direzione. In pratica, essi devono condividere una nozione di tempo che non si fermi mai e non torni mai indietro. Lo spazio mantiene la sua forma complessiva man mano che il tempo avanza, e non può frammentarsi in parti discontinue né creare i famosi tunnel spaziali come quello di Bajor. Stavolta le simulazioni al computer hanno dato loro ragione: su larga scala, l’universo così ottenuto ha proprio quattro dimensioni! La stabilità di questo universo richiede l’introduzione di una costante cosmologica, e ciò è in accordo con le osservazioni che confermano l’esistenza dell’energia oscura. Lo spazio-tempo da loro generato segue inoltre la Geometria di de Sitter, che è la soluzione delle equazioni di Einstein in un universo dotato di costante cosmologica.

Una delle novità più dirompenti di questo approccio consiste nel fatto che il numero di dimensioni dipende dalla scala a cui si osserva lo spazio-tempo! In altre parole, le simulazioni di breve durata dell’universo sembrano avere un numero di dimensioni diverso dalle simulazioni più lunghe. La cosa appare davvero stupefacente e contraria al senso comune, eppure non è del tutto esotica. Fino alla Lunghezza di Planck (8.2), per l’universo vale la classica Geometria di de Sitter a quattro dimensioni. Alla scala di Planck, invece, le fluttuazioni quantistiche diventano così forti, da compromettere la stessa nozione intuitiva di Geometria; il numero di dimensioni, dal valore classico di quattro, precipita a circa due. Tuttavia, lo spazio-tempo così ottenuto è ancora continuo ed è privo di tunnel spaziali che lo farebbero assomigliare ad una schiuma turbolenta. La sua geometria obbedisce a regole diverse da quelle classiche, ma il concetto di distanza si applica comunque. Una possibilità è che l’universo abbia una struttura frattale: un frattale è una struttura autosimile, che cioè ha lo stesso aspetto a tutte le scale a cui la si guarda. L’aggettivo auto simile, applicato al nostro universo, ci dice che esso avrà lo stesso aspetto a tutte le scale sotto una certa soglia: in questo caso, lo spazio-tempo non sarebbe fatto né di stringhe né tanto meno di atomi di spazio e tempo, ma sarebbe una regione di ripetitività infinita: la struttura osservata appena al di sotto della soglia semplicemente ripeterebbe se stessa ad ogni scala più piccola, fino all’infinito.

Ma non basta. Una nuova, suggestiva teoria promette di risolvere l’essenziale incompatibilità tra meccanica quantistica e relatività generale attribuendo al tessuto dello spazio-tempo le proprietà di un fluido con una viscosità bassissima, cioè di un superfluido. Come abbiamo visto, già la Gravità Quantistica a Loop pensa allo spazio-tempo come una complessa sostanza costituita nel suo intimo da elementi più piccoli, da “atomi” di spazio-tempo se così si può dire. In questo caso, le proprietà dello spazio-tempo dovrebbero “emergere” dalla fisica di base dei suoi costituenti, proprio come le proprietà dell’acqua derivano dalla fisica che governa le particelle che la compongono. « L’acqua è fatta di singole molecole che interagiscono tra loro secondo le leggi della meccanica quantistica; ma l’acqua liquida appare un continuo, fluido, trasparente e rifrangente », ha spiegato Ted Jacobson dell’Università del Maryland a College Park. « Queste sono tutte proprietà che non possono essere trovate nelle singole molecole, anche se, in ultima analisi, derivano da esse ». Per sapere se davvero lo spazio-tempo ha le caratteristiche tipiche di un fluido come l’acqua, occorre naturalmente confrontare le osservazioni astrofisiche con le previsioni basate su tale modello; ma non è facile ottenere risultati significativi, perché uno spazio-tempo di tipo fluido non sarebbe immediatamente distinguibile dalla spazio-tempo di un’altra teoria quantistica della gravità.

A questo proposito Stefano Liberati, della Scuola Internazionale Superiore di Studi Avanzati (SISSA) di Trieste, insieme al collega Luca Maccione della Ludwig-Maximilians-Universität di Monaco di Baviera, ha studiato in che modo questa struttura ideale possa influenzare la luce che viaggia attraverso l’universo, e si sono concentrati su situazioni estreme, che coinvolgono fotoni molto energetici. Essi potrebbero viaggiare attraverso lo spazio-tempo come le onde in un oceano, e si potrebbero applicare le leggi della meccanica dei fluidi e della fisica della materia condensata. In precedenza altri fisici hanno considerato in che modo come particelle di diverse energie verrebbero disperse nello spazio-tempo, proprio come le onde di diverse lunghezze d’onda si disperdono, o si propagano a velocità diverse, nell’acqua. In quest’ultimo studio invece Liberati e Maccione hanno preso in considerazione un altro fenomeno tipico dei fluidi: la dissipazione. Come le onde che si propagano in un mezzo, anche le particelle perdono energia nel tempo, e questo effetto frenante potrebbe riguardare anche i fotoni che viaggiano attraverso lo spazio-tempo. Anche se l’effetto è piccolo, fotoni molto energetici che viaggiano su enormi distanze dovrebbero perdere una notevole quantità di energia.

I due studiosi in particolare hanno preso in considerazione la Nebulosa del Granchio, il residuo di una supernova esplosa nel 1054 d.C. che dista circa 6.500 anni luce dalla Terra e che emette raggi X ad alta energia e raggi gamma. Con il passare tempo, questa luce raggiunge i nostri telescopi: la sua energia dovrebbe essersi dissipata in qualche misura se lo spazio-tempo ha effettivamente le proprietà di un liquido. Le osservazioni invece non mostrano alcun segno di tale fenomeno. « Nel nostro studio mostriamo che lo spettro di radiazione sarebbe notevolmente influenzato da questa perdita di energia perché viaggia per molto tempo, anche se si tratta di un effetto molto limitato », ha sottolineato Stefano Liberati. La mancanza di effetti di dissipazione ha permesso di porre forti vincoli sugli effetti liquidi che potrebbero essere presenti nello spazio-tempo, mostrando che essi devono essere estremamente piccoli o del tutto assenti, restringendo le possibilità di uno spazio-tempo fluido a liquidi con viscosità molto basse, che quasi non bagnano le superfici: i superfluidi, per l’appunto.

Se è vero che i fotoni di energie differenti viaggiano a velocità diverse e dissipano energia col passare del tempo, allora la Relatività non può valere in tutte le situazioni. Uno dei fondamentali principi della Teoria della Relatività Ristretta afferma che la velocità della luce è una constante universale, indipendente dal moto del sistema di riferimento in cui si trova l’osservatore. « L’idea che lo spazio-tempo come noi lo conosciamo emerga da qualcosa che viola la relatività è piuttosto radicale », ha ammesso Jacobson. Quest’ultimo e molti altri suoi colleghi tuttavia continuano a battere questa strada, poiché essa consentirebbe in linea di principio di risolvere alcuni dei problemi di incompatibilità tra la relatività generale e la meccanica quantistica. In ogni caso, se lo spazio-tempo è davvero un superfluido, i fisici teorici sono attesi da una difficilissima navigazione su di esso.

Altre teorie più o meno stravaganti per quantizzare la gravitazione sono quella del dilatone o graviscalare, nata applicando il formalismo di Feynman alla Teoria di Kaluza-Klein, la Teoria dei Torsori proposta nel 1967 da Roger Penrose e successivamente integrata in una variante della Teoria delle Superstringhe, e la Gravità Indotta del famoso fisico russo Andrei Sakharov (1921–1989), basata sull’analogia tra alcuni aspetti della Relatività Generale e il comportamento di certi cristalli. Tutte queste innumerevoli proposte per giungere ad una quantizzazione della gravitazione soffrono però di un grave difetto: gli effetti da esse previsti sono in genere troppo piccoli per poter essere sottoposti a verifica sperimentale. I Fisici tuttavia sperano che i nuovi telescopi orbitanti e i nuovi progetti per la ricerca delle onde gravitazionali ci offrano un giorno le risposte che cerchiamo, e ci aiutino a conquistare quel Santo Graal della Fisica Moderna che è l’unificazione definitive di tutte le forze, e quindi anche della sfuggente interazione gravitazionale.

Fonte: fmboschetto.it