La matematica è la chiave per comprendere e descrivere l’universo. Dopo aver dedicato un po’ di tempo a capire che la Terra come globo non può esistere, dobbiamo ora introdurre gli strumenti matematici che ci permetteranno di dare una descrizione significativa della Terra piatta. Lo scopo che ci prefiggiamo è infatti quello di descrivere e di misurare la Terra. Ovviamente tale misurazione non può essere fatta con un metro o con un qualsiasi strumento di misura. La misurazione dovrà essere fatta con strumenti concettuali di cui dobbiamo conoscere bene il significato. Il Pi Greco è uno di questi strumenti e ci consentirà di descrivere le misure della Terra e delle orbite dei corpi celesti.
Ci chiediamo quindi qual’è la precisione che vogliamo raggiungere nelle nostre operazioni di misura. Per far questo proviamo a ragionare al contrario. Voglio dire: è possibile riprodurre nel mondo reale tutte le astrazioni ideali possibili nel mondo matematico?
Pensiamo ad esempio ai numeri irrazionali. Questi sono numeri che non possono essere espressi con le frazioni. Un rapporto tra due numeri produce sempre un numero razionale che ha un numero finito di cifre dopo il punto.
Il numero di Nepero è irrazionale. Tutte le radici quadrate di numeri quadrati non perfetti sono irrazionali e infine il Pi Greco è un numero irrazionale. Il Pi greco è il rapporto tra la circonferenza e il diametro di un cerchio e può essere calcolato in molti modi diversi.
Un esempio è la serie di Leibniz:
Un’altro è la serie di Nilakantha:
Queste serie dovrebbero andare all’infinito, ma, quando le tagliamo ad un certo punto per un qualsiasi motivo pratico, stiamo razionalizzando Pi, rendendolo spiegabile e riproducibile come una singola frazione.
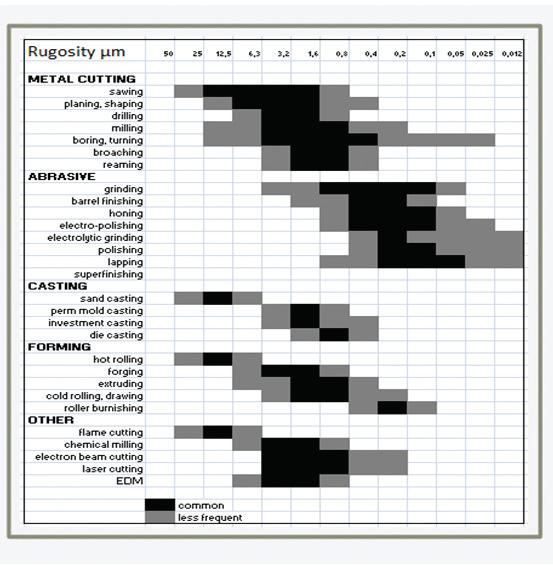
Perché un numero irrazionale non è riproducibile nella vita vera? Perché tutte le tecnologie, anche le più precise, hanno una precisione limitata e non possono replicare un numero con cifre infinite dopo l’unità. Riporto di seguito una tabella sulla precisione che può essere raggiunta con macchine utensili standard.
Quando lucidiamo una superficie, possiamo raggiungere una precisione di 0,01 micron.
Ciò significa che, quando vogliamo produrre un pezzo di acciaio lungo una quantità di millimetri pari al Pi greco, saremo in grado di produrre una lunghezza di 3,14159 mm ma niente di più preciso perchè ci manca la tecnologia, e probabilmente il denaro per sostenere lavorazioni via via più costose.
Quindi, si deve necessariamente razionalizzare, cioè tagliareun numero quandolo si vuole riprodurre come un vero oggetto. Razionalizzare significa tagliarlo in una frazione finita.
C’è un film: “Pi, Faith in Chaos” di Darren Aronofsky (davvero interessante), che termina con il numero Pi espresso come una frazione semplice. Nell’ultima scena in cui Jenna, la giovane ragazza cinese, si avvicina a Max in un parco, ponendo domande di matematica, propone un problema che rimarrà senza risposta: quanto vale 748 diviso 238? La risposta dovrebbe essere una buona approssimazione di PI, ma Max sorride e si siede semplicemente sulla panchina del parco osservando l’oscillazione delle foglie degli alberi.
Ciò emerge dopo una ricerca estesa e difficile del lungo numero che avrebbe dovuto avere il potere di fornire una descrizione finale dell’universo. Dopo questo “taglio” o razionalizzazione, Max Cohen sembra raggiungere la pace che prima mancava.
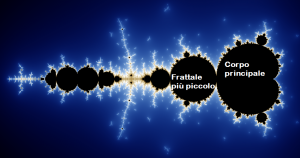L’idea è che l’universo potrebbe, forse, essere descritto con una precisione che, passo dopo passo, corre verso l’infinito, ma esiste un corpo principale, una base, forse il 95% del totale (3/3,1415 = 0,95), che devi prima trovare, solo per afferrare e comprendere il significato nascosto nella realtà che vediamo. Nella descrizione dell’universo dovremmo essere soddisfatti quando fossimo arrivati a trovare quell’intero, tagliato e approssimato nel punto giusto, che ci permette di capire la natura intima della realtà in osservazione.
Dati più precisi devono essere considerati frattali, una ripetizione del corpo principale su scala ridotta. I dettagli saranno studiati in un secondo momento con la consapevolezza che nessuno arriverà a comprendere, con assoluta precisione, l’intera creazione: “Solo Dio è perfetto” è una dichiarazione degna di nota nel film di Aronofsky.
Allo stesso modo la Bibbia, in Ecclesiaste 3:11, afferma: « Dio ha fatto ogni cosa bella al suo tempo: egli ha perfino messo nei loro cuori il pensiero dell’eternità, sebbene l’uomo non possa comprendere dal principio alla fine l’opera che Dio ha fatta.».
Ci sarà sempre un frattale più piccolo da studiare, ma fino a quel punto si deve razionalizzare (tagliare) per trovare il frattale più grande. Il rischio, al contrario, potrebbe essere quello di non trovare la descrizione corretta, nemmeno per le parti più visibili e più grandi della realtà in cui viviamo.
In Meccanica, ad esempio, è consuetudine linearizzare vicino al punto di lavoro ciò che non è lineare. Lo si fa usando la serie Taylor che può essere tagliata quando necessario. La funzione non lineare diventa una sorta di funzione lineare principale più una parte trascurabile che è un ordine di grandezza più piccolo della parte principale. Il piccolo errore commesso è considerato trascurabile, ma anche necessario per consentire la comprensione della funzione in modo più semplice.
Quindi, come puoi razionalizzare Pi? Nella tabella riportata ci sono alcune frazioni che possono essere usate per esprimere PI e l’errore che commettiamo usando quel rapporto.
Tutte queste frazioni sono approssimazioni del valore reale di Pi. Ognuna di queste frazioni è riproducibile con crescente difficoltà man mano che l’errore che facciamo diminuisce.
Anche il tempo deve essere considerato, perché ogni indagine scientifica ha bisogno di partire dal primo grande frattale, prima di passare a quello minore e così via.
Abbiamo visto che il Pi greco viene descritto per il 95% del suo valore intero dal numero 3. Tagliare il Pi greco a 3,14 vuol dire essere leggermente più precisi, ma non ci consentirebbe di afferrare appieno il primo frattale nella descrizione della Terra.
Notevole è il fatto che anche nella Bibbia il Pi greco vale 3. In 2 Cronache capitolo 4 verso 2 si descrive il bacino di rame fuso che si trovava vicino al tempio. Esso viene descritto in questo modo: “Fece la vasca di metallo fuso del diametro di dieci cubiti, rotonda, alta cinque cubiti; ci voleva una corda di trenta cubiti per cingerla.” Il rapporto tra circonferenza e diametro è il Pi greco e qui abbiamo 30/10=3. Faremo spesso riferimento alla Bibbia nella nostra descrizione della Terra, essendo la Bibbia un libro che parla di Terra piatta e vedremo che la Bibbia utilizza spesso numeri tronchi, in cui i frattali minori vengono trascurati.
Quindi, proprio come una prima approssimazione, per definire e descrivere i principali frattali che delineano la Terra, il sole, la luna, le stelle e tutto il firmamento in orbita attorno alla Terra, dovremmo tenere presente questa regola: il Pi Greco vale 3, più altri frattali minori.
Michele Vassallo è un ingegnere meccanico. Nel 2015, quando scoprì il movimento emergente degli American Flat Earthers, si sentì stupito e affascinato. Presto si rese conto che la Terra non poteva essere un globo. Nonostante il fatto che gli argomenti venuti alla ribalta fossero e siano ancora incompleti e contengano molti errori, il concetto generale di una terra piatta sembra assolutamente degno di indagine.
Tra le sue migliori scoperte c’è la reintroduzione dell’etere nella fisica della terra piatta e una nuova visione della natura della luce.
E’ coautore del libro “The real measures of the (flat) Earth” edito da Aracne editore e del blog “rifugiatidipella.com“. Dal 2019 produce materiale video inerente la Terra piatta sul suo canale Youtube “earthmeasured”.