In questo capitolo, proverò a fornire un riepilogo delle dimensioni della Terra usando tutte le informazioni elaborate negli articoli precedenti e aggiungerò alcune informazioni sulle mappe utilizzate per descrivere la Terra piatta.
Il punto di partenza della mia ricerca era stato inizialmente la determinazione del raggio della Terra. La misura risultante è 19980 km che troviamo facendo il calcolo 111 km ∙ 180 ° = 19980 km. Abbiamo infatti 180° di latitudine sulla semicirconferenza del globo, e già da tempo abbiamo capito che un grado di latitudine sul globo vale 111 km sulla Terra piatta.
Possiamo così scrivere questa tabella utilizzando il pi greco uguale a tre:
| Raggio [km] | Circonferenza [km] | |
| Tropico del Cancro | 6660 | 39960 |
| Tropico del Capricorno | 13320 = 6660 x 2 | 79920 |
| Diametro esterno | 19980 = 6660 x 3 | 119880 |
Sul motivo per cui usiamo il Pi pari a 3 si veda l’articolo “Quanto vale il Pi greco sulla Terra piatta“.
Una grande conseguenza della geometria della Terra piatta è che non c’è simmetria tra la parte meridionale della Terra e quella settentrionale come invece avviene su una sfera. Questo significa che nascono dei problemi nella traduzione delle latitudini e longitudini dal globo alla Terra piatta. Ciò è dovuto al fatto che i paralleli si allargano in modo continuo man mano che ci si allontana dal Polo Nord.
Qui vorrei mostrare al lettore la differenza di estensione tra la superficie della cosiddetta terra globulare e quella della superficie totale della terra piatta, dal polo nord fino all’Antartide. La superficie della sfera (con un raggio di 6371 km e π= 3,1415) sarebbe di 510.064.365 km2. D’altra parte, l’estensione della terra piatta con un raggio di 19980 km corrisponderebbe a una superficie di 1.197.601.200 km2, che è molto più del doppio.
Vediamo ora brevemente come si possono tradurre le coordinate del globo in coordinate polari date dal raggio misurato dal Polo Nord e un angolo ϑ in sostituzione della longitudine. Nella rappresentazione della Terra piatta, dobbiamo generare un insieme di coordinate per sostituire la latitudine e la longitudine del globo. Latitudine e longitudine creano un reticolo in tutto il globo che consente di definire la posizione di ciascun punto della Terra.
Su un disco, come quello definito dalla Terra piatta, useremo un insieme di coordinate polari, ovvero una distanza o un raggio misurato dal Polo Nord e un angolo misurato da un raggio di riferimento, ad esempio quello che passa attraverso Greenwich. Il raggio r dovrebbe sostituire la latitudine mentre l’angolo ϑ sostituisce la longitudine.
Per trasformare la latitudine, un angolo, in una distanza, dovremmo ricordare che un grado di latitudine corrisponde a 111 km sulla Terra piatta.
Un meridiano è infatti lungo 40000 km che, se diviso in 360 parti, fornisce 111 km per ogni grado di latitudine.
L’angolo ϑ corrisponde invece all’angolo di longitudine. Dovremmo tuttavia aggiungere una considerazione. La scienza postula la simmetria tra l’emisfero nord e sud. Aggiustano quindi latitudine e longitudine in base a questi calcoli. Vedremo in un prossimo articolo un esempio di calcolo applicato all’Australia. Noi quindi dobbiamo rivedere le coordinate in modo da costruire un modello coerente.
Quindi, consideriamo un esempio veloce che riprenderemo in futuro in modo più approfondito. La distanza su una superficie del globo tra, diciamo, Sydney (longitudine 151 ° EST) e Perth (115 ° EST), è di circa 3800 km mentre sulla Terra piatta, considerando la stessa latitudine, sarebbe di circa 8000 km. È chiaro quindi che ogni coordinata di longitudine per i luoghi nell’emisfero meridionale dovrebbe essere rivista. Basterebbe viaggiare in auto da Sidney a Perth per verificare che la distanza corretta è di 3900 km proprio come risulta dal Globo. Per avere un’idea della correzione che dovrebbe essere fatta, possiamo fare dei calcoli usando i numeri che abbiamo trovato fino ad ora.
Sul tropico del Cancro abbiamo 6660 ∙ π ∙ 2/360 = 6660 ∙ 3 ∙ 2/360 = 111 km per ogni grado di longitudine, essendo 6660 il raggio di quel tropico.
Sul tropico del Capricorno abbiamo 13320 ∙ π ∙ 2/360 = 6660 ∙ 2 ∙ 3 ∙ 2/360 = 222 km per ogni grado di longitudine.
Sulla circonferenza dei ghiacci attorno alla Terra abbiamo che 19980 ∙ π ∙ 2/360 = 6660 ∙ 3 ∙ 3 ∙ 2/360 = 333 km per ogni grado di longitudine.
Sulla circonferenza interna della cupola abbiamo 26640 ∙ π ∙ 2/360 = 6660 ∙ 4 ∙ 3 ∙ 2/360 = 444 km per ogni grado di longitudine.
Sulla circonferenza esterna della cupola abbiamo che 33300 ∙ π ∙ 2/360 = 6660 ∙ 5 ∙ 3 ∙ 2/360 = 555 km per ogni grado di longitudine.
Tenendo presente queste distanze, la differenza di longitudine tra Sidney e Perth dovrebbe essere di circa 3900/222 = 18 ° e non 36 ° (151 ° -115 °) come sarebbe sulla superficie di una terra globulare. E’ evidente quindi che nella descrizione della Terra piatta dovremmo rivedere tutte le longitudini, in modo da conservare le corrette distanze.
I greci furono i primi a descrivere la Terra come un globo. I loro filosofi iniziarono immaginando il sole al centro dell’universo. Essi usarono il globo come simbolo di tutto il cosmo. In effetti le dimensioni della traiettoria solare sono ribaltate nelle dimensioni del globo. Da allora, i re sono stati rappresentati con il globo in mano per mostrare il loro potere. Il globo era visibile insieme a statue e quadri, un esempio del quale è l’Atlante Farnese conservato a Napoli.
Questa è una statua del secondo secolo, che rappresenta la sfera celeste come un globo. A proposito, la prima mappa del globo terrestre conservata è l’Erdapfel, creato da Martin Behaim nel 1492. Il continente americano non era rappresentato, ma la Terra era, tuttavia, rappresentata come un globo. L’idea di una Terra sferica divenne sempre più diffusa.
Durante la successiva era dei grandi marinai e dei viaggi oceanici, avere la Terra rappresentata su mappe divenne sempre più necessario. Ciò significava che la sfera doveva essere disegnata su carte piatte. Mercatore è noto per aver creato una delle più famose di queste mappe. È conosciuta come la mappa di proiezione di Mercatore del 1569. Era una mappa “conforme” studiata per la navigazione. Conforme significa che la proiezione conserva gli angoli come sul globo e questa era considerata una caratteristica utile durante la navigazione.
Una mappa conforme è caratterizzata da una grande deformazione della Terra man mano che la latitudine cresce. Qualunque sia la proiezione della Terra su una mappa induce deformazioni dovute alla doppia curvatura del globo. Un cilindro ha una singola curvatura e può essere facilmente proiettato su un piano ma una sfera è diversa.
Questo vale anche per la proiezione di Mercatore. Un problema ben noto di questa proiezione, che è così diffusa in tutto il mondo, è che allarga molto le nazioni del nord, lasciando altre zone, come l’Africa, più piccole di quanto non siano in realtà. Come possiamo chiaramente immaginare, la rappresentazione geografica del mondo è stata usata come una sorta di strumento di propaganda per scopi sociali e politici.
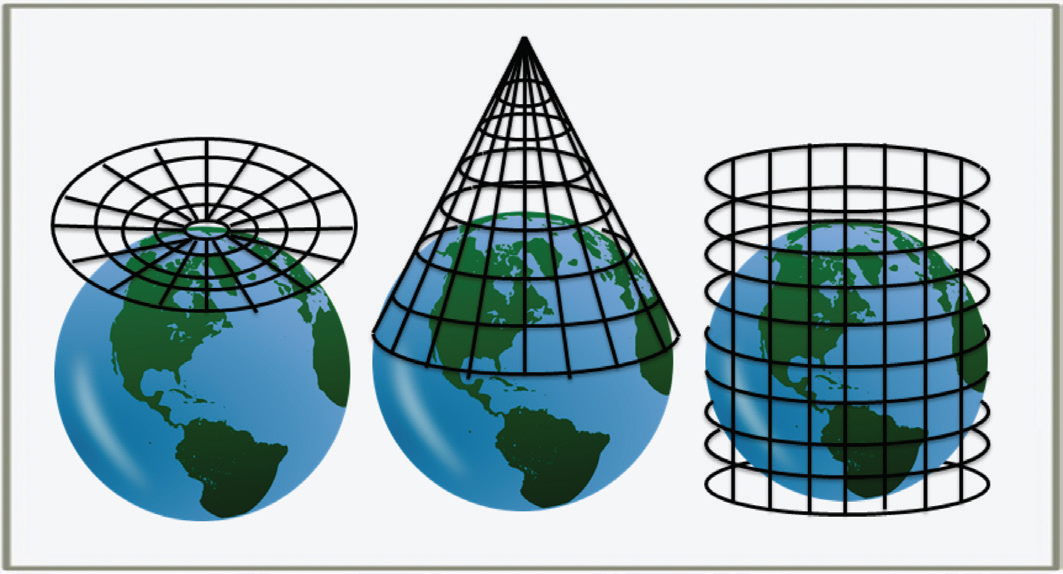
Tutte le mappe piatte della Terra presentano un grande difetto originale: il globo. Dal momento che tutti i geografi e cartografi consideravano, mentre svolgevano il loro lavoro, la Terra come un globo, rappresentavano la Terra a partire dalla sfera. Tutte le mappe successive sono solo proiezioni trasferite dal globo su un piano o su una singola superficie di curvatura come un cono o un cilindro. Questi possono essere facilmente appiattiti dopo essere stati proiettati dal globo.
Poiché tutte le mappe sono ottenute in questo modo, con una proiezione, vengono trasferite grandi deformazioni in tutte quante. La Terra è piatta ma un grande travisamento venne introdotto quando essa venne descritta come un globo e una seconda imprecisione venne introdotta quando il globo fu appiattito su una mappa. Spesso questa seconda trasformazione rende il primo errore ancora più grande e diventa impossibile tornare a capire e rappresentare la realtà così come essa effettivamente è.
Proviamo a commentare un po’ la mappa che viene spesso utilizzata per descrivere la Terra piatta: la proiezione equidistante azimutale centrata sul Polo Nord. È chiaro che, tra tutte le proiezioni, questa è la più adatta per mostrare la disposizione delle terre quando si vuole rappresentare la Terra piatta.
Il Polo Sud è tutto intorno alla Terra, il Polo Nord è al centro, gli angoli tra i meridiani vengono preservati e tutte le distanze misurate a partire dal Polo Nord sono uguali a quelle del globo. In confronto al globo, si manifestano grandi deformazioni della parte meridionale della Terra. La circonferenza del Polo Sud, per esempio, è enorme rispetto al polo sud del globo.
Chi conosce un po’ le vere misure della Terra riconosce che le distanze nell’emisfero meridionale descritte dalla mappa azimutale equidistante non sono corrette. Sorprendentemente, questa mappa, nonostante tutti i suoi meriti, non descrive perfettamente le vere misure. La mappa Azimutale o mappa di Gleason è infatti una semplice proiezione ottenuta dal globo.
Le mappe possono essere:
—— convenzionali, se le direzioni da un punto sono conservate; l’angolo tra due direzioni nella mappa è lo stesso nel globo;
—— equivalenti, se le aree della mappa sono le stesse nel globo. la forma sarà deformata;
——equidistanti, se le distanze lungo una certa direzione vengono preservate.
La mappa azimutale equidistante conserva l’angolo dei meridiani (azimut) ma anche le distanze dal Polo Nord. Questa mappa è disegnata dalla proiezione di tutti i punti che si sviluppano su un piano tangente al Polo Nord del globo.
Considereremo ora questa proiezione confrontandola con il nostro modello di Terra piatta. Nel nostro modello, il Tropico del Cancro si trova a 6660 km dal Polo Nord. Sul globo, la situazione è diversa e quindi anche sulla proiezione azimutale. Sul globo, abbiamo per ogni grado di latitudine 111,1 km. La latitudine del tropico è di 23,4 ° che significa 66,6 ° dal polo. Il tropico è quindi a 66.6 x 111.1 = 7400 km dal Polo Nord. La differenza è di 740 km con un errore del 10% che non è un piccolo errore. Ma ricorda che ci siamo occupati dei frattali e i numeri che abbiamo trovato sono solo il primo frattale. Potrebbe essere questo il motivo dell’errore?
6660 + 666 + 66.6 + 6.66 +… ≈7400 km L’errore ora è quasi zero.
L’equatore sul nostro modello si trova a 11100 km dal polo. Sul globo è a 90 ° x 111.1 = 10000 km. La differenza è di 1100 km con un errore dell’11%.
Ma potrebbe essere: 11100–1110–111–11.1–1.11≈9967 con un errore molto piccolo anche qui.
Quando si considera il nostro modello, il Capricorno è a 13320 km dal polo. Sul globo, dobbiamo calcolare (90 ° + 23,4 °) x 111,1 = 12600 km. La differenza è di 720 km con un errore del 5,7%. Ma anche qui dobbiamo considerare più di un solo frattale:
13320–666–66,6–6,66–0,666≈12580 km
Se è vero che rispetto alle latitudini gli errori sembrano essere minimi o nulli, il discorso diventa molto diverso con le longitudini. Il concetto è che con questa mappa introduciamo degli errori ed essa non dovrebbe quindi essere utilizzata se non per una descrizione qualitativa della Terra piatta. Vedremo meglio questo concetto nel prossimo articolo.
Michele Vassallo è un ingegnere meccanico. Nel 2015, quando scoprì il movimento emergente degli American Flat Earthers, si sentì stupito e affascinato. Presto si rese conto che la Terra non poteva essere un globo. Nonostante il fatto che gli argomenti venuti alla ribalta fossero e siano ancora incompleti e contengano molti errori, il concetto generale di una terra piatta sembra assolutamente degno di indagine.
Tra le sue migliori scoperte c’è la reintroduzione dell’etere nella fisica della terra piatta e una nuova visione della natura della luce.
E’ coautore del libro “The real measures of the (flat) Earth” edito da Aracne editore e del blog “rifugiatidipella.com“. Dal 2019 produce materiale video inerente la Terra piatta sul suo canale Youtube “earthmeasured”.