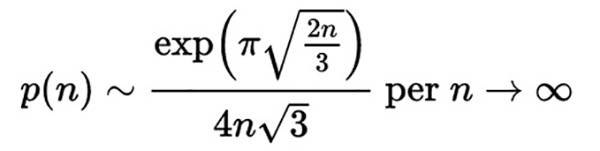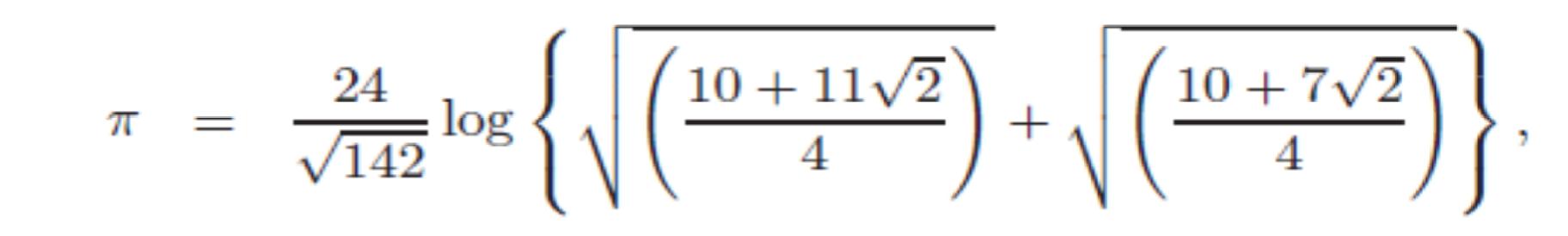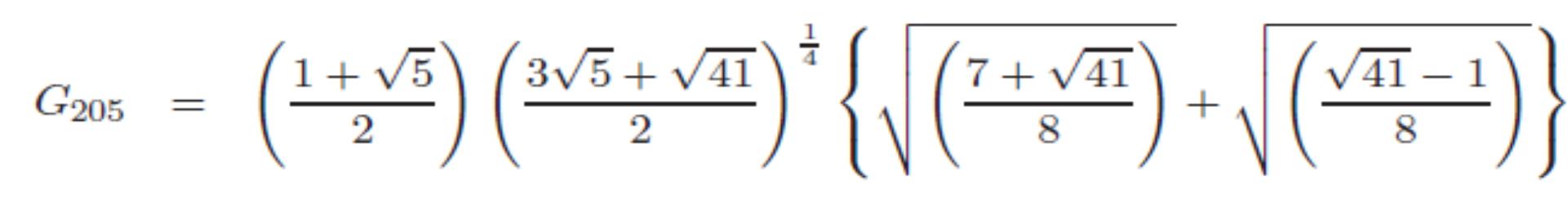
Verso una teoria del tutto?
Da circa un anno stiamo studiando ed approfondendo molte delle innumerevoli formule e diversi teoremi (più di 5000) elaborati dal genio indiano Srinivasa Ramanujan. Nel corso della nostra analisi, spessissimo abbiamo trovato formule che sono strettamente connesse a π, φ e a ζ(2)=(π^2)/6=1.644934…, cioè a Pigreco, al rapporto aureo φ = (√5 + 1) / 2 e a zeta(2). Ramanujan ha fornito contributi geniali all’analisi matematica e alla teoria analitica dei numeri, lavorando su argomenti complessi ed estesi come le funzioni ellittiche, le serie infinite e le frazioni continue. Teorie ed equazioni che hanno avuto conseguenze oltre che in numerosi campi della matematica, anche in vari settori della fisica e della cosmologia. Una di esse è legata ai numeri di Bernoulli. In matematica, i numeri di Bernoulli costituiscono una successione di numeri razionali che gioca un ruolo importante in vari problemi. Accanto ad essi conviene prendere in considerazione i polinomi di Bernoulli che si possono considerare una loro generalizzazione. Essi hanno applicazioni in molti campi della matematica quali, per esempio, l’analisi, il calcolo numerico e la teoria dei numeri.
I numeri di Bernoulli, compaiono nell’espressione di certi valori della Funzione Zeta di Riemann, il cui andamento risulta legato alla distribuzione dei numeri primi. Una delle proprietà scoperte da Ramanujan è che i denominatori delle frazioni dei numeri di Bernoulli sono sempre divisibili per 6. Nella sua famosissima lettera al matematico G .H. Hardy, Ramanujan sostiene di aver fatto progressi su una teoria di serie divergenti e di aver risolto il problema della distribuzione dei numeri primi. Due risultati presentati da Ramanujian riguardano le serie infinite e il valore di pi greco. Le lettere che Ramanujan ha scritto ad Hardy nel 1913 contenevano molti affascinanti risultati. Ramanujan ha lavorato sulle serie di Riemann, sugli integrali ellittici, sulle serie ipergeometriche e le equazioni funzionali della funzione zeta. Il contributo più famoso e fondamentale riguarda il teorema sul numero p(n) delle partizioni di un intero nei suoi addendi. Se chiamiamo p(n) la funzione che ci dice qual è il numero di partizioni per n, Ramanujan e Hardy proposero nel 1918 una formula asintotica per calcolare il valore di questa funzione,
Una formula che fu migliorata nel 1937 da Hans Rademacher. I suoi primi, e insoliti risultati, come i numeri primi di Ramanujan e la funzione teta di Ramanujan (utilizzata nella teoria delle stringhe e per studiare la termodinamica dei buchi neri), hanno ispirato una grande quantità di ricerche successive. (wired.it). Altro argomento trattato da Ramanujan e da noi approfondito è lo studio delle funzioni mock theta, le equazioni modulari e le approssimazioni a π. Le funzioni mock theta fanno parte di un insieme di funzioni, nominate da Srinivasa Ramanujan, nel campo della teoria dei numeri e delle funzioni modulari, in una lettera scritta in punto di morte a G. H. Hardy . Le funzioni mock theta costituiscono una serie infinita di numeri, probabilmente correlate alle funzioni theta, note da secoli e usate in un gran numero di problemi e analisi matematiche. In particolare, comportamenti descrivibili con funzioni mock theta sono oggi stati individuati in diversi campi: nei calcoli matematici, fisici, chimici.
Riguardo alle approssimazioni a π, svariate e affascinanti sono le formule che Ramanujan ci ha lasciato. Diamo qui due esempi, a nostro parere molto interessanti:
Come è evidente, nella espressione che fornisce un’ottima approssimazione a π, compare il numero 24 (8×3) che nella matematica di Ramanujan appare ripetutamente. La cosa che teniamo ad evidenziare è che la funzione di Ramanujan appare anche nella teoria delle stringhe. Come afferma il fisico Michio Kaku “ognuna delle 24 modalità nella funzione di Ramanujan corrisponde ad una vibrazione fisica della stringa”.
Nella espressione denominata nel lavoro di Ramanujan G205 , compare (√5 + 1) / 2, che è uguale al valore di φ = 1.61803398….Molte equazioni modulari, se si effettua l’estrazione di radici ennesime, forniscono come risultati ottime approssimazioni a ζ(2) =(π^2)/6=1.644934..quindi a zeta(2) connessa alla funzione zeta di Riemann, che a sua volta è saldamente legata ai numeri primi. Riemann ha scoperto che la funzione zeta ha un collegamento molto stretto con la distribuzione dei numeri primi e, in particolare, la posizione dei suoi zeri è legata alla possibilità di contarli in modo accurato. Ricordiamo che, per quanto riguarda i valori assunti da ζ(x), lo stesso Eulero calcolò i valori di ζ(x) per x intero positivo pari, da 2 a 26; ad esempio, egli provò che:
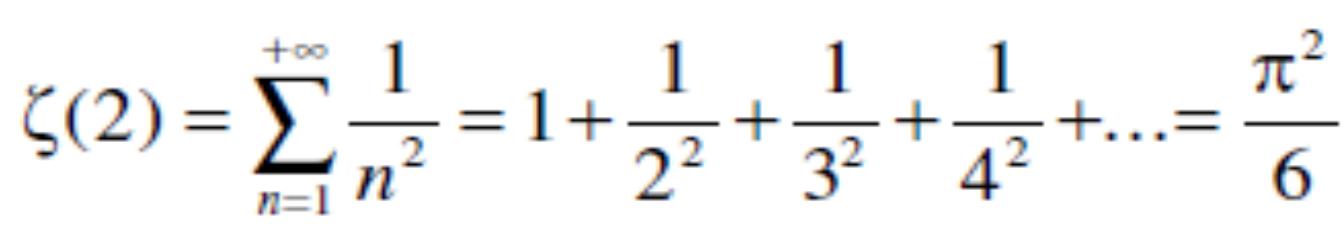
Numeri di Bernoulli, funzione zeta di Riemann, numeri primi, serie infinite, partizioni, funzioni mock ed equazioni modulari: cosa può legare tutti questi argomenti? Vi è un qualcosa che li unisce? E il rapporto aureo?
Perché è praticamente onnipresente nella matematica di Ramanujan questo interessantissimo valore che gioca un ruolo chiave in molti settori della fisica e della cosmologia?
Nei nostri studi sui buchi neri, argomento in cui vengono utilizzate varianti delle formula per le partizioni di Hardy-Ramanujan, abbiamo osservato che per qualunque temperatura, massa e raggio di Schwarzschild che vengono inseriti in una formula che abbiamo sviluppato, il risultato è SEMPRE un valore vicinissimo a quello del rapporto aureo (solitamente 1.61808 che è praticamente quasi uguale al valore di φ = 1.61803398…). Inoltre, quando si cercano le connessioni tra le equazioni di Ramanujan e le varie formule inerenti i vari settori della fisica delle particelle, della teoria delle stringhe e della cosmologia, molte proprietà fisiche, ad esempio la massa del mesone π (Pione) o del Bosone di Higgs, si ottengono sviluppando le formule attraverso l’uso dei numeri primi, e/o dei numeri appartenenti alle serie di Fibonacci e di Lucas, che sono connesse al valore del rapporto aureo.
Secondo il nostro parere, la chiave di tutto è nella dinamica dei frattali. Anche Nassim Haramein afferma: ”Vedete frattali molto specifici che si riferiscono e obbediscono al rapporto aureo di 1.618, che emerge direttamente dalla struttura del vuoto. Nell’Universo frattale l’unica cosa che esiste è il punto. In ogni punto tutta l’informazione è disponibile. Ogni punto contiene il Tutto” (Nassim Haramein).
Haramein afferma che l’Universo nell’intero, obbedisce alla condizione che descrive un buco nero. Ha sviluppato vari grafici di scala che supportavano il concetto di un Universo-buco nero-frattale. Dal suo punto di vista, l’infinita forza nucleare forte era il risultato dell’attrazione gravitazionale di mini-buchi neri e fu un’estrema conferma scoprire che, considerando un protone come un buco nero, l’energia necessaria per renderlo una tale entità era l’energia tipicamente associata con la forza forte. Immaginiamo tutti gli atomi che compongono il nostro corpo fisico e l’intero mondo materiale attorno a noi, fatto di mini-buchi neri della dimensione del protone. Non prima del 2008 venne pubblicata una prima versione dei calcoli, in un lavoro intitolato: “Scale Unification: A Universal Scaling Law for Organized Matter”. Una versione più completa intitolata: “The Schwarzschild Proton”, venne presentata ad una conferenza scientifica in Belgio nel 2009, dove ha vinto il “Best Paper Award” (Nassim Haramein).
Questo può essere connesso alla matematica di Ramanujan ed alle connessioni che si ottengono con diverse proprietà delle particelle, delle stringhe e delle più disparate proposte e teorie di cosmologia? Certamente sì, soprattutto se comprendiamo come la matematica di Ramanujan, molto avanti, rispetto al tempo in cui fu concepta, è lo schema iniziale, il fondamento di una possibile Teoria del Tutto che se vuole essere tale dovrà necessariamente tenere conto di π, φ, ζ(2), dei numeri primi e delle successioni di Fibonacci e Lucas che, a nostro avviso, sono le “informazioni” che portano, ciclo dopo ciclo, alla nascita di un Multiverso Frattale come quello in cui viviamo.