Il discorso da noi avviato a proposito delle galassie ci porta direttamente a discutere della struttura dell’universo secondo Dante, cioè della cosmologia dantesca. Ma attenzione: non stiamo parlando del sistema geocentrico tolemaico, da noi sviluppato ampiamente in un’altra lezione, perchè quest’ultimo rappresenta la struttura del Sistema Solare. Stiamo riferendoci invece all’idea stessa che Dante aveva di spazio.
Il discorso da noi avviato a proposito delle galassie ci porta direttamente a discutere della struttura dell’universo secondo Dante, cioè della cosmologia dantesca. Ma attenzione: non stiamo parlando del sistema geocentrico tolemaico, da noi sviluppato ampiamente in un’altra lezione, perchè quest’ultimo rappresenta la struttura del Sistema Solare. Stiamo riferendoci invece all’idea stessa che Dante aveva di spazio.
Appare più che legittimo domandarsi cosa vi è al di là delle stelle, considerate a buon diritto l’orizzonte dello sguardo che l’uomo può gettare sul cosmo. Secondo il poeta romanesco Giuseppe Gioachino Belli (1791-1863), proprio questo fu il motivo per cui gli uomini avrebbero deciso la costruzione della Torre di Babele:
«Pe vede’ cosa c’e’ ssopra le stelle
Che sse po’ ffà?” diceveno le gente.
Fece uno: “E che ce vò? Nun ce vò gnente:
frabbichiamo la torre di Babbelle»
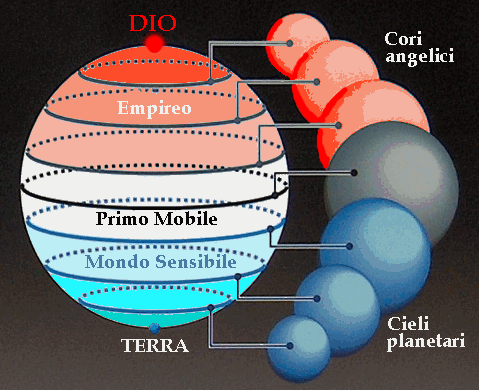
All’epoca di Dante le stelle erano ritenute tutte equidistanti dalla superficie terrestre, ed incastonate su di una sfera, il firmamento appunto. Ispirandosi alla dottrina di Aristotele, al di là di esso era stato posto il Primo Mobile, che non conteneva alcun astro visibile, ma originava il movimento degli altri cieli, come visto parlando della planetologia dantesca. Ma al di là del Primo Mobile vi era ancora qualcosa? Evidentemente sì.
I teologi introdussero allora il cielo Empireo (dal greco “empyros”, “infuocato”), il più alto dei cieli, luogo della presenza fisica di Dio, dove risiedevano gli angeli e le anime beate: in pratica, esso coincideva con il Paradiso. Ed infatti più volte Beatrice ricorda che esso è la sede naturale dei Beati, i quali si mostrano a Dante lungo i diversi Cieli dei Pianeti solo per dargli modo di constatare i diversi gradi di beatitudine. Secondo alcuni, le stelle altro non erano che fori nella sfera del firmamento, attraverso cui filtrava la luce eterna dell’Empireo posto al di là di esso. La sua origine va ricercata nella Bibbia, dove è usata l’espressione semitica “Cieli dei Cieli” per indicare il più alto degli spazi, dove risiede il Signore Dio in persona:
«O regni della terra, cantate a Dio,
salmeggiate al Signore,
a Colui che cavalca sui cieli dei cieli eterni!
Ecco, egli fa risuonare la sua voce,
la sua voce potente» (Salmo 68, 32-33)
«Lodatelo, cieli dei cieli,
e voi acque al di sopra dei cieli!» (Salmo 148, 4)
Dante parla di questo Cielo Supremo già nel Convivio:
«E quieto e pacifico è lo luogo di quella somma Deitade che sola [sè] compiutamente vede. Questo loco è di spiriti beati, secondo che la Santa Chiesa vuole, che non può dire menzogna; e Aristotile pare ciò sentire, a chi bene lo ‘ntende, nel primo De Celo et Mundo. Questo è lo soprano edificio del mondo, nel quale tutto lo mondo s’inchiude, e di fuori dal quale nulla è; ed esso non è in luogo ma formato fu solo ne la prima Mente, la quale li Greci dicono Protonoè. Questa è quella magnificenza de la quale parlò il Salmista quando dice a Dio: Levata è la magnificenza tua sopra li cieli» (Convivio II, III, 10-11)

L’Empireo era dunque concepito infinito ed illimitato, anzi privo affatto di dimensioni fisiche, e non costituito da materia, neppure dalla purissima quintessenza, come si credeva fossero gli altri cieli: era una realtà di puro spirito, fuori dal tempo e dallo spazio, e mentre i nove cieli erano in perpetuo movimento, come una sorta di orologio cosmicoe, l’Empireo era eternamente immobile ed immutabile. Dante viaggia attraverso di esso negli ultimi quattro canti della Divina Commedia, e quando vi entra Beatrice così glielo descrive:
«Noi siamo usciti fore
del maggior corpo al ciel ch’è pura luce:
luce intellettüal, piena d’amore;
amor di vero ben, pien di letizia;
letizia che trascende ogne dolzore.
Qui vederai l’una e l’altra milizia
di paradiso, e l’una in quelli aspetti
che tu vedrai a l’ultima giustizia.» (Paradiso XXX, 38-45)
Nell’Empireo insomma Dante vedrà entrambe le schiere del Paradiso, quella degli Angeli e quella dei Santi, e quest’ultima ha modo di vederla come essa apparirà nel giorno del Giudizio Finale, quando ogni anima «ripiglierà sua carne e sua figura» (Inf. VI, 98). Le tribune su cui siedono i Beati appaiono a Dante disposte lungo una “candida rosa”. Nell’Empireo inoltre il nostro poeta ha modo di contemplare le gerarchie degli angeli, disposte su nove cerchi concentrici, ad immagine dei nove cieli; e al centro di questi nove cerchi, un punto luminosissimo che rappresenta la Divinità, in cui Dante arriva a scorgere i misteri della Trinità e dell’Incarnazione.
In pratica, quando l’Alighieri comprende «me sormontar di sopr’a mia virtute» (Par. XXX, 57), cioè che le sue facoltà percettive sono accresciute più di quanto egli stesso non credeva possibile, si rende conto che sta guardando una sorta di secondo universo, simmetrico rispetto al primo, costituito dal mondo sensibile! Quest’ultimo infatti è composto da nove cieli materiali che circondano la Terra; l’Empireo a sua volta è formato da nove cieli, stavolta spirituali, che convergono loro pure in in un punto.
A complicare la questione della “cosmologia su larga scala” di Dante viene il fatto che in alcuni passaggi l’Empireo sembra circondare il Primo Mobile e quindi il mondo sensibile, così come vediamo raffigurato su tutte le nostre edizioni della Divina Commedia (ed anche noi ne abbiamo visto un esempio):
«Luce e Amor d’un cerchio lui comprende,
sì come questo li altri; e quel precinto
Colui che ‘l cinge solamente intende.» (Par. XXVII, 112- 114)
Cioè: il cerchio di luce e d’amore che è l’Empireo contiene il Primo Mobile, così come quest’ultimo comprende tutti i cieli precedenti; e solo Colui che lo avvolge, cioé Dio, intende cosa sia e in che modo operi. Appena un canto dopo, invece, l’Empireo sembra piuttosto “richiudersi su se stesso”, come se esso non fosse lo spazio esterno ad una sfera (il Primo Mobile), ma piuttosto lo spazio interno ad essa!
«Distante intorno al punto un cerchio d’igne
si girava sì ratto, ch’avria vinto
quel moto che più tosto il mondo cigne;
e questo era d’un altro circumcinto,
e quel dal terzo, e ‘l terzo poi dal quarto,
dal quinto il quarto, e poi dal sesto il quinto.
Sopra seguiva il settimo sì sparto
già di larghezza, che ‘l messo di Iuno
intero a contenerlo sarebbe arto.
Così l’ottavo e ‘l nono; e chiascheduno
più tardo si movea, secondo ch’era
in numero distante più da l’uno;
e quello avea la fiamma più sincera
cui men distava la favilla pura,
credo, però che più di lei s’invera.
La donna mia, che mi vedëa in cura
forte sospeso, disse: “Da quel punto
depende il cielo e tutta la natura.”» (Par. XXVIII, 25-42)
Dante Alighieri sta osservando il punto luminosissimo nel quale riconoscerà l’Unità e Trinità di Dio, e vicino ad esso vede girare un cerchio di fuoco (“d’igne”), tanto veloce da superare anche il moto di quel cielo (il Primo Mobile) che più rapidamente si volge intorno alla Terra.
Questo primo alone è circondato (“circumcinto”, latinismo) da un secondo, e questo da un terzo, e via seguitando. Il settimo è così esteso che persino “il messo di Iuno”, cioè l’arcobaleno, se anche fosse un circolo intero e non un arco, quale noi lo vediamo (vedi la lezione dedicata all’Ottica), sarebbe troppo stretto (“arto”) per contenerlo. Ed ognuno si muove con velocità decrescente, in proporzione del numero d’ordine di ciascuno in rapporto all’unità: il secondo ha velocità angolare pari alla metà del primo, il terzo la ha pari a un terzo del primo, e così via, proprio come il Cielo della Luna è più veloce di quello di Mercurio, questo di quello di Venere, e così via, potenziando la simmetria tra mondo materiale ed Empireo.
E risplende più limpida (“sincera”) la fiamma di quel cerchio che ruota più vicino alla “favilla pura”, cioè a Dio, perchè, essendo più prossimo alla perfetta Verità che Egli è, maggiormente si compenetra in essa. Il commento di Beatrice (“Da quel punto / depende il cielo e tutta la natura”) riflette quasi letteralmente la formula aristotelica «Ex tali igitur principio dependet coelum et natura» (Metafisica XII, 7), ripresa da San Tommaso nella Summa Theologica; ma Dante sostituisce all’astratto “principio” il concetto di “punto geometrico” (del quale riparleremo in seguito)
Se dunque nel Canto XXVII il Primo Mobile appariva come un cielo la cui struttura fisica non è dissimile da quella degli altri cieli, cioè una sfera esterna e concentrica a quelle planetarie e stellari, immersa nell’infinità dell’Empireo, che delimita l’intero Universo visibile, appena un centinaio di versi dopo lo stesso Empireo viene raffigurato come un’altra serie di sfere concentriche, costituite dai vari ordini di angeli che ruotano a loro volta attorno ad un punto centrale che è Dio stesso.
Guardando dal Primo Mobile verso l’esterno, cioè verso l’Empireo, è come se ci trovassimo a contemplare un… secondo universo, simmetrico rispetto al mondo sensibile, con nove cieli intorno a un fulcro di rotazione che resta immobile!! Nessuno ha rappresentato artisticamente questa situazione meglio di Sandro Botticelli (1445-1510), il celebre autore della “Primavera” cui Lorenzo il Magnifico nel 1490 commissionò le illustrazioni per una nuova edizione della Divina Commedia:
Curiosamente, il nostro Autore si sofferma a sottolineare con forza come non vi sia alcuna indicazione che si debba scegliere un punto particolare sul Primo Mobile per avere questa visione; anzi, Dante ci ha già avvisati che il Primo Mobile è così omogeneo ed isotropo (cioè sempre uguale a se stesso in ogni punto e in ogni direzione, che non riesce a stabilire con certezza neppure da che parte vi è entrato:
«Le parti sue vivissime ed eccelse
sì uniforme son, ch’i’ non so dire
qual Bëatrice per loco mi scelse.» (Par. XXVII, 100-102)
Con questa terzina, il Ghibellin Fuggiasco vuole dirci che avremmo la stessa visione dell’interno dell’Empireo guardando “fuori” da qualsiasi punto del Primo Mobile. In altri termini, se posso dir così, l’Empireo è un Cielo che circonda l’universo sensibile, e allo stesso tempo è a sua volta richiuso a mo’ di sfera intorno ad un punto. Apparentemente siamo davanti ad una contraddizione, che comunque nella geometria euclidea è impossibile da spiegare. E allora?
E allora, l’unica spiegazione possibile è quella proposta per la prima volta nel 1925 dal matematico tedesco Andreas Speiser (1885-1970) nel suo “Klassische Stücke der Mathematik”: lo spazio del Paradiso Dantesco è basato su una geometria non euclidea!!!
L’ipotesi non è così peregrina come potrebbe parere a prima vista, dato che l’Alighieri aveva probabilmente più familiarità con la geometria sferica, legata alle osservazioni astronomiche, che con la geometria euclidea: forse fu questo a favorire la sua arditissima intuizione di una geometria “diversa”. Ma cosa vuol dire, esattamente, “geometria non euclidea”? Nel capitolo dedicato alla Geometria Euclidea abbiamo parlato con ampiezza del Quinto Postulato di Euclide. Fin dal tempo del suo autore, questo assioma fu oggetto di dibattiti a non finire. Se infatti i primi quattro appaiono praticamente evidenti nella loro chiara semplicità:
- I) Per due punti passa una retta ed una sola
- II) Un segmento che congiunge due punti può essere prolungato indefinitamente
- III) Dato un punto e un segmento vi è un solo cerchio che ha l’uno come centro e il secondo come raggio
- IV) Tutti gli angoli retti sono uguali tra loro
altrettanto non si può dire per il quinto, del quale si conoscono differenti enunciati, tutti equivalenti fra di loro (come è possibile dimostrare), ma nessuno dei quali appare evidente a prima vista:
Se una retta taglia altre due rette determinando dallo stesso lato angoli interni la cui somma è minore di quella di due angoli retti, prolungando le due rette, esse si incontreranno dalla parte dove la somma dei due angoli è minore di due angoli retti (enunciato originale di Euclide)
Date due rette parallele tagliate da una trasversale, la somma dei due angoli coniugati interni è pari ad un angolo piatto
Data una retta qualsiasi r ed un punto P non appartenente ad essa, è possibile tracciare per P una ed una sola retta parallela alla retta r data (il cosiddetto enunciato di Playfair)
In un quadrilatero ABCD avente due angoli e retti e i lati uguali, anche gli altri due angoli sono retti (enunciato di Saccheri)
In un triangolo la somma degli angoli interni è pari ad un angolo piatto (l’enunciato da noi visto a proposito del triangolo con due angoli ottusi)
Non tutti i matematici dunque accettarono a cuor leggero l’indimostrabilità di questo postulato, e cercarono per secoli di dedurlo dai primi quattro. Tra questi vi fu Padre Gerolamo Saccheri (1667-1733), il quale nella sua opera “Euclides ab omni nævo vindicatus” (“Euclide ripulito da ogni difetto”, 1733) tentò di negarlo, nella speranza di poterlo dimostrare per assurdo. Egli credette di esserci riuscito, ma in realtà aveva dedotto nient’altro che una nuova geometria, che obbediva a teoremi completamente diversi da quelle della geometria euclidea, e perciò detta geometria non euclidea. Dopo la morte di Saccheri la sua opera fu dimenticata, poiché nessuno se la sentiva di mettere in dubbio la geometria di Euclide, confortata dall’evidenza.
Tuttavia il tedesco Carl Friedrich Gauss (1777-1855), uno dei più grandi matematici di ogni tempo, la riscoprì, la rivalutò e tentò di costruire ex novo una geometria non euclidea, ma non pubblicò mai i suoi risultati. A giungere per primi ad una geometria non euclidea compiuta, indipendentemente l’uno dall’altro, furono il russo Nikolaj Lobacevskij (1793-1856) nel 1829 e l’ungherese Janos Bolyai (1802-1860) nel 1832. Essi fondarono il lavoro su un postulato completamente diverso dal Quinto di Euclide:
Per un punto fuori di una retta passano infinite rette parallele ad una retta data.
Come realizzare in pratica questa strampalata geometria? In realtà è meno difficile di quanto sembri: basta chiamare “piano” quello che per Euclide è un cerchio, e “retta” ogni corda dello stesso cerchio (estremi esclusi). È facile verificare che i primi quattro postulati di Euclide valgono anche in questa geometria. Tuttavia, non vale più il famoso Quinto Postulato se definisco “rette parallele” due corde del cerchio che non si intersecano mai. Si consideri infatti la seguente figura:
Il punto P non appartiene alla “retta” AB, ma come si vede ci sono infinite “rette” passanti per P (ad esempio r1, r2, r3) che non intersecano AB, e quindi ad esse “parallele”! Questa nuova geometria viene chiamata iperbolica. Si può dimostrare che in essa valgono ancora molti teoremi della geometria euclidea: ad esempio gli angoli opposti al vertice sono congruenti, ma non è più vero che la somma degli angoli interni di un triangolo è pari a 180° (questo infatti è uno degli enunciati alternativi del
Quinto Postulato): è invece sempre minore di 180°. Un’ottima rappresentazione di una geometria iperbolica di questo tipo è stata fornita dal pittore olandese Maurits Cornelis Escher (1898-1971) nella sua straordinaria opera “Limite del cerchio III” (1959): ponendoci al centro del disegno e smuovendoci verso il bordo di esso, ci restringiamo sempre di più, e per raggiungere il bordo ci occorrerà percorrere una distanza infinita, proprio come se volessimo raggiungere il “bordo” di un piano euclideo. Questa rappresentazione dell’infinito anticipa di qualche decennio la formulazione matematica del concetto di frattale ad opera di Benoit B. Mandelbrot (1924-1910).
Successivamente, sempre negando il Quinto Postulato, Bernhard Riemann (1826-1866) nel 1854 costruì un’altra geometria non euclidea, stavolta detta ellittica, in cui vale il seguente postulato alternativo:
Per un punto fuori di una retta non si può condurre alcuna retta ad essa parallela.
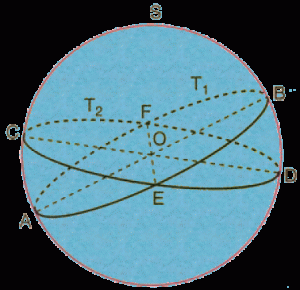
Come riuscire in questa impresa? Basta chiamare “piano” quella che per Euclide è la superficie di una sfera S, e “rette” i suoi cerchi massimi, ad esempio T1 e T2, mentre “punti” sono le coppie di punti euclidei antipodi sulla sfera, come ad esempio E ed F nella figura seguente:
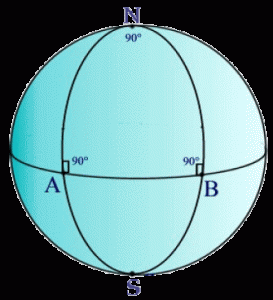
Come si vede, nessun cerchio massimo può evitare di intersecarne un altro, e dunque le rette parallele non esistono più, in accordo con il “nuovo” postulato di Riemann! Non è difficile dimostrare che in questa geometria non esistono triangoli simili, salvo quando sono anche congruenti; che da un punto ad una “retta” si possono condurre infinite perpendicolari; che due “rette” perpendicolari ad una stessa “retta” non sono parallele tra loro; e soprattutto che la somma degli angoli interni di un triangolo è sempre maggiore di 180°. Infatti si consideri la superficie terrestre e si prendano il suo equatore e due meridiani separati da 90° di longitudine.
Come si vede qui sotto, il triangolo ABN formato dall’intersezione di questi tre cerchi ha ben tre angoli retti, e quindi la somma dei suoi angoli interni è pari a 270°! La geometria costruita sulla superficie di una sfera è una geometria non euclidea!
Come si vede, mentre la geometria iperbolica di Lobacevskij e Bolyai sfrutta pur sempre figure piane come il cerchio che si sostituiscono al piano, invece la geometria ellittica di Riemann abbandona il piano, costruendo la sua geometria su di una superficie curva. In questo caso si tratta in effetti della superficie tridimensionale di una sfera, ma il tutto può essere generalizzato ad una “superficie ad n dimensioni”, che prende il nome di varietà riemanniana n-dimensionale. Viene introdotto in tale modo il concetto di curvatura dello spazio, giacché la varietà di Riemann è manifestamente una superficie curva. In particolare, la sfera viene chiamata una “varietà di Riemann a curvatura positiva”, in quanto la somma degli angoli interni di un triangolo risulta maggiore di un angolo piatto.
Allora la geometria euclidea, che è costruita dentro un piano, è una geometria a curvatura nulla, mentre la geometria iperbolica prima descritta è una “varietà di Riemann a curvatura negativa”, in quanto la somma degli angoli interni di un triangolo risulta minore di un angolo piatto. In pratica, la geometria costruita su una superficie sferica è sicuramente ellittica, mentre quella costruita su di un piano è inevitabilmente euclidea, e quella realizzata su di una superficie “a sella” è certamente iperbolica, come mostra lo schema seguente:
La grande intuizione di Andreas Speiser è stata proprio questa: l’universo di Dante non è uno spazio euclideo, bensì una varietà di Riemann! Ecco come si esprime egli stesso:
«Dante possiede una chiara visione globale della complessa struttura spaziale nella sua totalità. Per le nove sfere del cielo, Dante recupera la rappresentazione di Aristotele, apportando un cambiamento fondamentale che riguarda la fine dello spazio: come può essere che la sfera più distante, che appare la più grande, abbia in realtà le più piccole dimensioni? […] Lo spazio di Dante è una varietà di Riemann con una fonte di energia che imprime ad esso la metrica» (“Klassiche stücke der Mathematik”, 1925)
La forma dell’Universo di Dante secondo Speiser è quella che i matematici chiamano ipersfera, cioè una sfera avente più di tre dimensioni: nel nostro caso quattro. Il nostro cervello è incapace di figurarsi oggetti con più di tre dimensioni, ma possiamo avere un’idea del modello di Speiser se procediamo per analogia con quanto avviene nello spazio euclideo ordinario. Se consideriamo una comune sfera tridimensionale, la quale secondo i matematici ha la topologia di una due-sfera (perché sulla sua superficie si può camminare in due direzioni, nord-sud ed est-ovest), partendo dal polo sud verso l’equatore notiamo che i paralleli su di essa si allargano sempre più fino all’equatore; poi, man mano che procediamo verso il polo nord, rimpiccioliscono di nuovo fino a ridursi ad un punto. Tutti i paralleli presi globalmente costituiscono la due-sfera.
Analogamente, se a partire da un punto prendiamo una serie di sfere di raggio crescente, fino ad arrivare ad un valore massimo dopo il quale esse cominciano a ridursi sino a ridursi nuovamente un punto, potremo dire che tutte queste sfere hanno costruito una tre-sfera, cioè una sfera quadridimensionale con una superficie a tre dimensioni, di cui il punto iniziale rappresenta il polo sud, il punto final rappresenta il polo nord, e la sfera di raggio massimo rappresenta l’equatore. Ci accorgiamo così di avere fra le mani una bizzarra sfera quadridimensionale, la cui superficie è costituita da una successione di infinite sfere tridimensionali! Il punto da cui partiamo è la Terra (anzi, il centro della Terra); le sfere di dimensione crescente sono le sfere dei quattro elementi e poi le sfere celesti fatte di etere, cioè il mondo sensibile; l’equatore della tre-sfera è costituita dal Primo Mobile; le successive sfere decrescenti sono i cori angelici, puramente spirituali, che costituiscono l’Empireo; il punto di arrivo è Dio.
Se ancora non siete riusciti a figurarvi una geometria di questo genere, ricorriamo ad un’altra immagine, elaborata dal giornalista Carlo Rovelli. Consideriamo la superficie della nostra Terra: una tecnica molto semplice per disegnarla su una carta geografica piana, quindi bidimensionale, consiste nel disegnare due dischi, uno comprendente i continenti dell’emisfero boreale e con il polo nord al centro, e l’altro con l’emisfero australe centrato sul polo sud.
L’equatore risulterà disegnato due volte, rappresentando il bordo di entrambi i dischi. Se partiamo dal polo sud e ci muoviamo verso nord, a un certo punto attraverseremo l’equatore, e saremo costretti a “saltare” da un disco all’altro. Nella realtà non facciamo alcun salto, perché noi sappiamo bene che l’emisfero boreale, visto da chi proviene dal polo sud, “circonda” l’emisfero australe, così come l’emisfero australe “circonda” quello boreale, per chi guarda da nord. L’ipersfera può essere rappresentata in maniera del tutto analoga, disegnando due serie di sfere, una delle quali di raggio crescente rappresenta “l’emisfero australe” della tre-sfera, l’altra di raggio decrescente simboleggia “l’emisfero boreale”.
La sfera “equatoriale” che al tempo stesso separa e connette i due emisferi costituisce il termine della prima serie e l’inizio della seconda. Un viaggiatore che, come Dante, partirà dal centro della prima serie e salirà “di sfera in sfera” fino a questo equatore, vedrà sotto di sé un insieme di sfere concentriche, che si richiudono intorno ad un punto. Quest’altro emisfero allo stesso tempo “circonderà” e “sarà circondato” dalla prima serie!
Un’indiscutibile conferma di questa straordinaria visione quadridimensionale dell’universo ci è offerta dallo stesso Dante quando, appena entrato nell’Empireo oltrepassando il Primo Mobile, l’ultima frontiera dell’universo materiale, afferma:
«Non altrimenti il trïunfo che lude
sempre dintorno al punto che mi vinse,
parendo inchiuso da quel ch’elli ‘nchiude,
a poco a poco al mio veder si stinse» (Par. XXX, 10-13)
Il punto di luce e le sfere di angeli circondano l’Universo sensibile, e insieme sono circondati dall’Universo stesso! Nessuna altra spiegazione è possibile, se non quella che ne ha dato Speiser, e che oggi è condivisa da molti matematici e fisici. Tra questi vi è lo scienziato romeno Roman Patapievici (1957-), direttore dell’Istituto di Cultura della Romania, il quale ha fatto notare come Dante colga per un attimo l’accecante visione di Dio circondato dai cori angelici, usando gli occhi di Beatrice come uno specchio.
Ma l’immagine allo specchio è simile a quella reale, solo che è invertita. Il mondo invisibile diventa allora un «calco rovesciato del mondo visibile»: l’Empireo è Teocentrico mentre il nostro Universo è Geocentrico; i cori angelici orbitano intorno a Dio a velocità sempre più alta via via che ci si avvicina a Dio, mentre i cieli accelerano via via che ci si allontana dalla Terra; l’invisibile obbedisce a norme opposte rispetto al visibile. Dalla circonferenza massima di una sfera è possibile vedere ogni suo punto, sia in direzione del polo nord che del polo sud; analogamente, dalla sfera del Primo Mobile è possibile vedere tutti i cieli planetari e la Terra guardando da una parte, tutti i cori angelici e la Trinità Divina guardando dall’altra!
Ma quanto vi ho detto fin qui non esaurisce affatto l’argomento. Se infatti Dante è stato geniale nel descrivere l’ipersfera con tanta chiarezza, oltre 500 anni prima che venissero sistematizzate le prime geometrie non euclidee, nel concepire il suo “universo a specchio”, per metà avvolto intorno alla Terra e per metà attorno al punto da cui «Dante epende il cielo e tutta la natura» (Par. XXVIII, 42), egli andò addirittura al di là, anticipando le intuizioni cosmologiche dello stesso Albert Einstein. Per scoprire insieme a me come ciò fu possibile, passate alla lezione successiva.