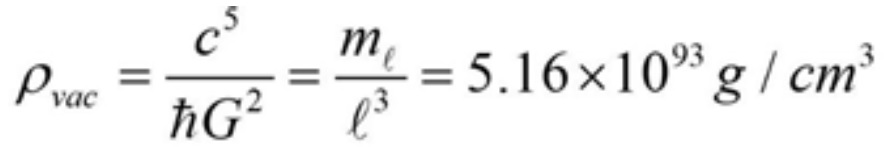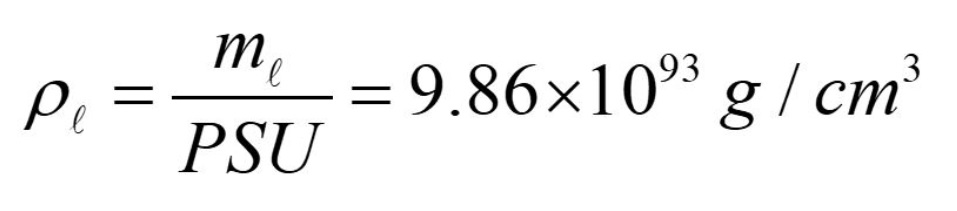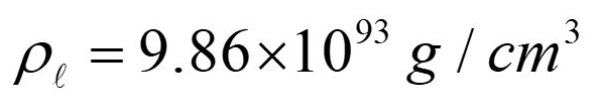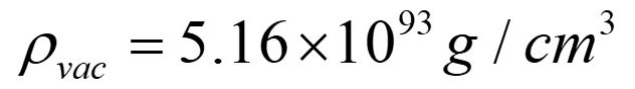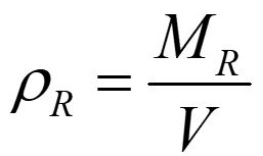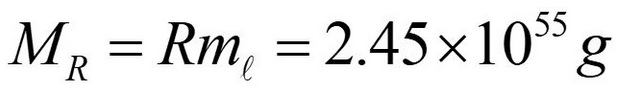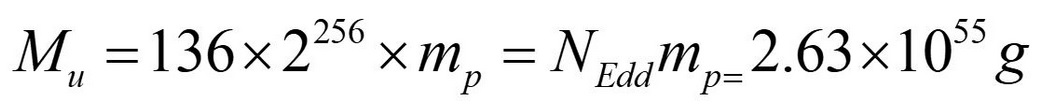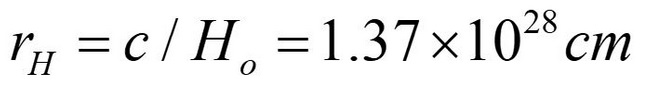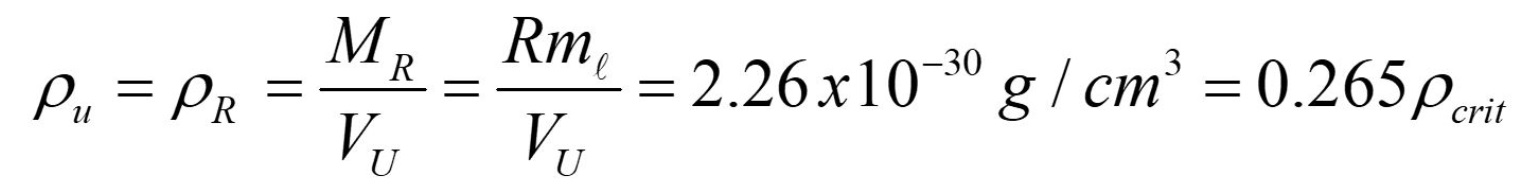In questo articolo affrontiamo la soluzione olografica proposta da Nassim Haramein per spiegare l’enorme differenza di 122 ordini di grandezza tra la densità dell’energia del vuoto a livello cosmologico e la densità predetta dalla teoria quantistica dei campi, la cosiddetta “Catastrofe del Vuoto” di cui abbiamo scritto nello scorso articolo. Il calcolo completo intitolato “Resolving the Vacuum Catastrophe: A Generalized Holographic Approach”, di Haramein e della Dr. Val Baker, è stato pubblicato nel Journal of High energy Physics, Gravitation and Cosmology, nel 2019. Per stimare la densità dell’energia del vuoto in scala quantistica , la teoria quantistica dei campi (QFT) descrive un vuoto composto da un numero infinito di campi elettromagnetici che fluttuano in tutte le frequenze (dette anche fluttuazioni del vuoto oppure oscillazioni di punto zero). Tramite l’effetto Casimir abbiamo prova sperimentale dell’esistenza di queste oscillazioni di punto zero. La QFT quindi calcola la densità del vuoto quantistico in ogni punto dello spazio, sommando le energie in tutte le frequenze di vibrazione ω.
Dato che in principio non c’è limite alle frequenze, ne abbiamo un numero infinito da sommare. Sommando il contributo di tutte le possibili frequenze arriviamo ad una densità infinita di energia in ogni punto dello spazio, a meno che non venga rinormalizzata al valore di taglio di Planck. Piuttosto che usare la somma di tutte le frequenze, la QFT determina una densità del vuoto alla scala di Planck, dividendo la massa di Planck ml = 2.18 x 10^-5 gr, per il volume di Planck, un cubo con V=l^3 (dove l è la lunghezza di Planck l= 1.616 x 10^-33 cm).
Come vediamo nella figura sotto, questo ci da un valore dell’energia del vuoto quantistico di
un valore supportato sia da risultati teorici che sperimentali.

Per risolvere la catastrofe del vuoto, dobbiamo prima capire da dove venga realmente il valore della densità di energia del vuoto alla scala di Planck.
Come abbiamo visto nella sezione 7.12 del nostro corso di scienza unificata, Nassim definisce un’area di Planck (2D), che è un’area circolare col diametro pari alla lunghezza di Planck, come “bit” o unità di informazione sulla struttura dello spaziotempo. Haramein generalizza questo concetto in una unità sferica (3D) di Planck, dove il bit è l’area equatoriale di questa PSU (Planck Spherical Unit), per risolvere le equazioni gravitazionali a livello cosmologico e quantistico. (1)
Come vedremo in seguito, la struttura fisica e quindi la densità di energia in questa scala, sono meglio rappresentate in PSU. Per calcolare questa densità p1 alla scala quantistica dobbiamo dividere la massa di Planck m1 per il volume di una PSU, di conseguenza la densità di energia del vuoto risulta,
Questa densità di energia del vuoto alla scala quantistica,
è leggermente maggiore del valore standard predetto dalla teoria quantistica dei campi discussa in un articolo precedente
che si ottiene rinormalizzando alla scala di Planck, utilizzando un cubo come volume dell’unità di spazio, invece di una sfera. Il modello olografico generalizzato descrive come un corpo sferico possa essere considerato in termini di impacchettamento di PSU (unità sferiche di Planck), che è anche la sua entropia di volume R. La massa-energia (o massa olografica) Mr è data in termini di PSU con l’equazione Mr=R m1 ( m1 è la massa di Planck , mentre R è calcolato dividendo il contenuto di PSU nel volume V, per il volume di una PSU, Vls.
La densità di massa-energia di un corpo sferico è data come
dove Mr è la massa e V è il volume del corpo sferico. Nel caso di un protone, la massa-energia (detta massa olografica) in termini di massa di Planck è calcolata come
dove R è calcolato dividendo il contenuto di PSU nel volume del protone Vp per il volume di una singola PSU. Questa quantità ci dice quante PSU possono riempire un protone, come vediamo nella figura sottostante.

Questa massa olografica risultante può essere considerata equivalente alla massa dell’Universo osservabile stimata da approcci cosmologici standard. Per esempio, il numero di Eddington (che stima il numero di protoni nell’Universo) moltiplicato per la massa del protone, ci fornisce la massa dell’Universo:
Dato che questi valori della massa dell’Universo osservabile sono solo approssimazioni, considereremo la massa dell’Universo osservabile come la massa-energia o massa olografica del protone Mr. La massa-energia dell’Universo può quindi essere calcolata in termini di densità di massa-energia del protone, dividendo questa massa per il volume dell’Universo
(valore ottenuto considerando l’Universo come una sfera e calcolando il suo volume Vu usando il raggio di Hubble come raggio dell’Universo ru).
Quindi, la densità di massa-energia del vuoto in scala cosmologica risulta essere
Il processo completo è rappresentato dalla figura seguente:

Vediamo che questo valore è 0.265 ρcrit molto vicino a 0.268 ρcrit che corrisponde alla densità di materia oscura. Quindi, se consideriamo la densità di energia del vuoto quantistico in termini di densità di protoni e impacchettamento di PSU, troviamo il divario di densità tra scala cosmologica e quantistica, 10^122.
Fermiamoci un momento per comprendere a pieno quanto abbiamo fatto. L’equazione di sopra prende una massa-energia del protone o massa olografica e la rende uguale a quella dell’Universo, quindi la inserisce in un volume maggiore, quello dell’Universo Vu. In questo modo otteniamo una densità di questo “protone dilatato alla dimensione dell’Universo” che risulta nella densità di massa oscura dell’Universo, come determinata dai correnti modelli cosmologici! Praticamente stiamo espandendo un protone che può essere considerato una singolarità (punto di densità di massa-energia estremamente elevata), dalla sua dimensione a quella dell’Universo..non vi suona familiare? Certamente, è il big-bang!
Tale risultato ha spinto facilmente Haramein a pensare che quanto noi chiamiamo big-bang è la conseguenza dell’espansione di un protone sfuggito da un precedente Universo , evento estremamente rapido a causa della pressione negativa creata dalla densità estremamente bassa presente all’esterno del precedente ambiente. Risultò anche evidente che l’enorme cambiamento di densità dovuto all’espansione del protone avrebbe creato un gradiente di densità, che proprio come per un tornado e il suo gradiente di pressione/temperatura, avrebbe fornito una fonte per la rotazione in tutte le scale, la fonte dello spin!
 Qualcosa di molto simile venne suggerito dall’astronomo Georges Lemaitre nel 1927 con la sua “teoria del Big Bang”, inizialmente chiamata “ipotesi dell’atomo primordiale”.
Qualcosa di molto simile venne suggerito dall’astronomo Georges Lemaitre nel 1927 con la sua “teoria del Big Bang”, inizialmente chiamata “ipotesi dell’atomo primordiale”.
Inoltre l’ipotesi di Haramein implicherebbe l’esistenza di Universi incorporati uno nell’altro, in modo simile al modello di Penrose (Cosmologia ciclica conforme – CCC), dove l’Universo si ripete in cicli infiniti, eone dopo eone e divenne uniforme prima e non dopo il Big Bang. Nel modello CCC ogni ciclo inizia come singolarità prima di espandersi e generare agglomerati di materia, che infine vengono risucchiati da buchi neri supermassicci, i quali scompariranno emettendo continuamente radiazione di Hawking. Questo processo ripristina l’uniformità e prepara la scena per il seguente Big Bang (ne parleremo nella prossima sezione).
In modo simile, la densità di energia del vuoto (da non confondere con la densità di massa-energia associata alla massa oscura) può essere considerata in termini di piastrellatura superficiale di PSU (entropia di superficie, η ) all’aumentare del raggio dalla scala di Planck a quella cosmologica. La densità del vuoto in scala cosmologica è data come.
Dove η si ottiene assumendo un Universo sferico di raggio ru . Il risultante cambio di densità, da quella alla scala di Planck a quella in scala cosmologica, porta all’esatto equivalente calcolato in precedenza, alla densità osservata Pcrit. Questa è la densità di energia del vuoto in scala cosmologica, ottenuta usando la soluzione olografica, che risponde a quanto definito come energia oscura.
Sommando i numeri degli esponenti delle densità dell’energia del vuoto quantistico (93) e del vuoto in scala cosmologica (30), otteniamo gli ordini di grandezza che separano le due densità: 93+30=121. Questo semplice calcolo risolve i ~122 ordini di grandezza tra il valore cosmologico e quello delle fluttuazioni alla scala di Planck, uno dei “grandi problemi della fisica”.

Quindi, quando usiamo l’approccio olografico generalizzato, che descrive come ogni corpo fisico possa essere considerato in termini di impacchettamento di PSU, mostriamo la relazione di scala tra le PSU e l’universo a guscio sferico e risolviamo i 122 ordini di grandezza tra la densità dell’energia del vuoto alla scala di Planck e quella in scala cosmologica. Da qui è bastato un piccolo salto per immaginare che tutta l’informazione nel tessuto dello spaziotempo durante l’espansione evolutiva del nostro universo, ha generato il lato “positivo” contraente del potenziale di energia (opposto al potenziale “negativo” dell’energia oscura), che corrisponderebbe direttamente al componente gravitazionale della struttura di massa-energia che genera il mondo fisico.
In termini semplici, quando l’universo si espanse dalla dimensione del protone alla sua dimensione attuale, il contenuto di informazione-energia della sua evoluzione (spaziomemoria) venne codificato nella struttura del vuoto, formando la materia che ora osserviamo come protoni o atomi nel nostro universo. Quando consideriamo una PSU come un bit di informazione, la soluzione alla catastrofe del vuoto è che l’espansione avviene perché l’Universo necessita di superficie ulteriore per conservare informazione nel suo volume. Per esempio, questa informazione può contenere le coordinate tra ogni PSU e qualsiasi relazione tra esse.
Prospettiva della Resonance Science Foundation
Abbiamo visto come la soluzione olografica generalizzata risponde alla misteriosa discrepanza tra la densità dell’energia del vuoto in scala quantistica e quella in scala cosmologica (“Catastrofe del Vuoto”), spiegando allo stesso tempo la natura dell’energia e della materia oscura. Dato che ogni PSU rappresenta anche un quanto di rotazione o di momento angolare (spin), accade che avendo una spiegazione per le fluttuazioni del vuoto e la relativa densità, abbiamo incluso lo spin intrinseco nel tessuto dello spazio. La materia oscura venne proposta come fonte aggiuntiva di attrazione gravitazionale che contribuisce alla stabilità strutturale delle galassie. Includendo lo spin nella struttura dello spazio, la componente centripeta dello stesso spin può agire da forza coesiva delle galassie. Anche l’energia oscura venne inventata per spiegare l’espansione accelerata dell’Universo, ma anche tale forza può essere attribuita alla componente centrifuga dello spin inerente alla struttura dello spazio, fornendo l’equivalente della costante cosmologica.
Il caffè è una analogia stupenda della confusione nella fisica cosmologica attuale. Quando guardi una tazzina di caffè, vedi tutto nero, ma aggiungendo latte e rotazione, osserverai una spirale, come la galassia nella foto qui sotto. Se consideri solo la dinamica del latte per comprendere la galassia, perderai il 95% del contenuto del sistema!
 La galassia non ruota per conto proprio, ma viene assistita dalla rotazione/spin del vuoto (il caffè nero). Nei nostri modelli correnti, il 95% è mancante, perché il 68% è energia oscura e il 27% è massa oscura. Se non considerate correttamente il caffè nella tazza, non potrete mai comprendere e descrivere il comportamento del latte! L’atrofisica attuale non riconosce il collegamento tra le galassie a distanza di milioni di Megaparsec. Non riescono a riconoscere che le galassie emergono dalla dinamica di un mezzo onnipresente in perpetua rotazione…lo spazio!
La galassia non ruota per conto proprio, ma viene assistita dalla rotazione/spin del vuoto (il caffè nero). Nei nostri modelli correnti, il 95% è mancante, perché il 68% è energia oscura e il 27% è massa oscura. Se non considerate correttamente il caffè nella tazza, non potrete mai comprendere e descrivere il comportamento del latte! L’atrofisica attuale non riconosce il collegamento tra le galassie a distanza di milioni di Megaparsec. Non riescono a riconoscere che le galassie emergono dalla dinamica di un mezzo onnipresente in perpetua rotazione…lo spazio!
Come fa notare Christian Corda (2), le teorie estese della gravità generano scenari inflazionistici che risolvono molti problemi, inclusa l’espansione accelerata. Questo concorda con la teoria qui presentata, dove l’accelerazione dell’Universo può essere spiegata in termini di gradiente di pressione causato dal potenziale di trasferimento di informazione all’orizzonte superficiale. Infine la soluzione della catastrofe del vuoto suggerisce uno scenario affascinante…ovvero che il nostro Universo soddisfi la condizione di Buco Nero, una volta che si considera il contributo delle fluttuazioni del vuoto! Lo spiegheremo in altro articolo.
Nota: questo articolo è ispirato al materiale scritto dalla Dr.Amira Val Baker ed è contenuto nella sezione 7.2 del nostro corso gratuito.
Autore: Dr. Inés Urdaneta, Physicist/ Research scientist at Resonance Science Foundation
Riferimenti
[1] N. Haramein, Phys. Rev. Res. Int., vol. 3, no. 4, pp. 270-292, 2013.
[2] C. Corda, “Interferometric detection of gravitational waves: the definitive test for General Relativity,” Int. J. Mod. Phys. D18, vol. 18, pp. 2275-2282, 2009.