Abbiamo visto nel primo articolo “L’accelerazione di Coriolis dimostra che la Terra non ruota” che l’effetto Coriolis non si manifesta sulla Terra come dovrebbe. L’obiezione che mi viene spesso fatta è che l’atmosfera verrebbe trascinata in rotazione insieme alla Terra e agirebbe sull’elicottero (vedi articolo precedente) con una forza laterale che annulla l’accelerazione di Coriolis. Per questo non sarebbe possibile vedere in modo sensibile il manifestarsi di tale effetto.

Vedremo comunque in questo articolo prove del fatto che l’atmosfera non ruota perché la Terra è ferma.
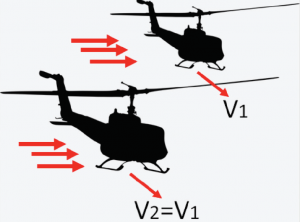
Quando si prova ad effettuare il calcolo, si noterà che, per un aereo o elicottero che vola a una velocità media di 500 km/h, l’accelerazione di Coriolis è di circa 0,0065 m/s². È un’accelerazione molto piccola. Se si considera una superficie laterale, offerta al vento dall’elicottero di 10 m² per una massa totale di 5000 kg, si raggiungerà una forza laterale necessaria del vento di 33 N (3,3kg), che davvero non sembra molto. Quindi, si potrebbe dedurre che sia possibile che l’atmosfera produca una sorta di vento laterale molto costante che costringa l’elicottero a muoversi, evitando così il manifestarsi dell’effetto Coriolis. Ma è davvero così?

Si consideri allora di avere due diversi elicotteri che iniziano insieme il loro viaggio dal Polo Nord all’equatore. Questi elicotteri abbiano la stessa massa, 5000 kg, e possano sviluppare la stessa velocità di 500 km / h. Ciò significa che in ogni momento del loro volo essi avranno percorso la stessa distanza. L’unica differenza tra i due elicotteri sia la geometria: uno sia più compatto e offra una superficie laterale alla spinta dell’atmosfera di 10 m², mentre l’altro offra una superficie laterale di 15 m².

L’accelerazione di Coriolis che l’atmosfera dovrebbe imprimere sui due elicotteri per mantenerli con la stessa velocità periferica della Terra è data dalla formula:

dove Ac è l’accelerazione di Coriolis ω è la velocità angolare della Terra e V_h è la velocità dei due elicotteri. Poiché V_h è lo stesso, è chiaro che è necessaria la stessa accelerazione per i due elicotteri. La forza necessaria per sviluppare tale accelerazione è data da Fc = m ∙ Ac.

Poiché la massa dei due elicotteri è la stessa, la forza necessaria è la stessa.

La pressione dovuta alla forza con cui l’atmosfera spingerebbe sul lato dei due elicotteri è tuttavia diversa. Poiché un elicottero è più grande dell’altro A1> A2 avremo che P1 <P2 secondo la formula P = F / A dove P è la pressione, F la spinta laterale data dall’atmosfera, pari a Fc, e A è la superficie laterale su cui l’atmosfera deve spingere.

Ma la pressione generata dall’atmosfera è collegata dalla velocità trasversale dell’atmosfera rispetto all’elicottero con la formula seguente con la quale possiamo calcolare la velocità necessaria dell’atmosfera.

dove ρ è la densità dell’aria pari a 1,25 kg/m³.

Poiché P1 e P2 sono diversi, troviamo che sono necessarie due diverse velocità dell’atmosfera V1 <V2. Questo non è possibile perché nello stesso punto (dove abbiamo entrambi gli elicotteri) possiamo avere una sola velocità dell’atmosfera.

Questa è una chiara prova che l’atmosfera non ruota e non agisce sull’elicottero per trascinarlo in rotazione con la Terra.

Consideriamo ora altri aspetti in relazione alla presunta spinta atmosferica.

– Il pendolo di Foucault.

Il suo movimento rotatorio è considerato la prova della rotazione della Terra. Mi dicono, i miei detrattori, che l’atmosfera ruota con la Terra. Obiettano che, nell’esempio dell’elicottero, essa è responsabile del trascinamento dell’elicottero in modo che questo non abbia a risentire dell’accelerazione di Coriolis.

Perché, dunque, nel caso del pendolo di Foucault, l’atmosfera non agisce su di esso? Perché non blocca la rotazione del pendolo che si muove in modo solidale con la Terra? L’obiezione dovrebbe essere valida anche nel caso del pendolo. Se l’atmosfera trascina l’elicottero dovrebbe anche trascinare il pendolo che quindi dovrebbe sempre muoversi sullo stesso piano di oscillazione. Invece si afferma che il pendolo muove su piani che ruotano a causa della rotazione della Terra attorno al proprio asse. Questa è una chiara dimostrazione delle incoerenze in cui si cade quando si vuole dimostrare che la Terra ruota. Evidentemente l’atmosfera non ruota.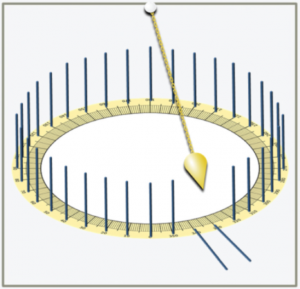

Ma cos’altro potrebbe essere aggiunto sull’argomento? Per quanto riguarda il pendolo di Foucault, intendo. Questa oscillazione è sempre usata come prova della rotazione della Terra. Ciò accade perché, nel corso del suo movimento, non segue il meridiano della terra. Ciò implicherebbe, per coerenza, che anche tu, quando sei seduto all’interno dell’elicottero, nel caso si fermasse per un breve periodo nell’aria, tu stesso, voglio dire, dovresti riuscire a vedere la Terra che si muove sotto i tuoi piedi. Ad ogni modo, questo non succede mai: non c’è coerenza dunque.

Molti esperimenti hanno dimostrato che il pendolo di Foucault funziona come previsto solo se lanciato in una direzione accuratamente scelta, con una forza iniziale specifica. Un lancio casuale non produrrà il movimento di rotazione previsto con i calcoli teorici che prevedono la rotazione della Terra. La conclusione è che il pendolo di Foucault non può essere considerato una prova della rotazione della Terra. Risulta inoltre chiaro che l’atmosfera non ruota e non agisce sul pendolo.

– L’esperimento di Guglielmini.

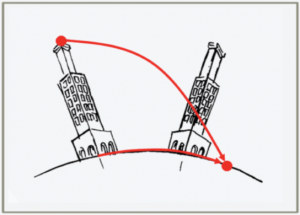
Per rimanere sull’argomento, potremmo anche discutere dell’esperienza di Guglielmini. Egli lanciò più volte una palla di piombo da una torre alta 100 m a Bologna. La storia racconta che, nel suo esperimento, egli vide che la palla cadeva con uno spostamento di 17 cm lontano dalla base della torre, verso est. La spiegazione è che la sommità della torre, essendo alta 100 metri, ha una velocità periferica di rotazione maggiore rispetto alla base, secondo la formula V = ω ∙ r. Questo esperimento sottolinea, ancora una volta, che un corpo nell’aria non viene trascinato dalla Terra o dall’atmosfera ma si muove con la velocità periferica del punto da cui ha iniziato il suo movimento, in questo caso la cima della torre.

Quindi, se l’esperienza di Guglielmini deve essere considerata valida, anche la nostra considerazione sull’aereo che trova impossibile seguire la Terra dovrebbe essere considerata valida. Come l’atmosfera non trascina con se la palla di piombo di Guglielmini, allo stesso modo non trascina con sé neanche l’elicottero. Questo è solo per evidenziare le incoerenze di chi vuole forzatamente dimostrare che la Terra ruota: provano ad arrampicarsi sui vetri ma non ci riescono.

Ma l’esperimento di Guglielmini è vero? Vediamo.

La boccia ha una velocità periferica corrispondente alla velocità periferica della parte superiore della torre. Il fondo della torre si muove a una velocità inferiore perché è più vicino al centro del globo.

C’è quindi un profilo di velocità triangolare come quello nella foto. La scienza afferma che la palla cade giù con la velocità periferica della cima della torre e che si muove verso est durante la sua caduta.

Come conseguenza di questo esperimento, se un elicottero si alza sulla sua verticale e rimane fermo, diciamo, per un’ora nello stesso punto, dovrebbe sentire la Terra muoversi sotto di se. Ciò dovrebbe accadere perché, quando l’elicottero si solleva, mantiene la velocità periferica della Terra, ma ad un’altitudine, diciamo, di 2000 metri, dovrebbe avere una maggiore velocità per mantenersi stazionario sullo stesso punto. (Il ragionamento è lo stesso fatto per la palla di Guglielmini che in punta alla torre ha una velocità periferica maggiore rispetto a quella della torre). Facciamo il calcolo supponendo che l’elicottero si trovi su un aeroporto situato all’equatore. L’equatore ha una velocità periferica di 1670 km/h con un raggio di 6378 km.

L’elicottero vola rimanendo sulla verticale a 2000 metri di altitudine. Calcoliamo la velocità che l’elicottero dovrebbe avere a quell’altezza, per rimanere sulla verticale.

Vp = ω ∙ r dove Vp è la velocità periferica e ω è la velocità di rotazione espressa in radianti al secondo.

ωterra = 7,27E^-5 rad / sec = 6.94E^-4 rpm

Vp = 7,27E^-5 * (6378000 + 2000) = 464 m / s * 3,6 = 1670,28 km/h

Δ = 1670.28-1669.3≈1 km/h

La differenza, come puoi immediatamente notare, è molto piccola: solo 1 km / h, ma significa che, se l’elicottero rimane nella stessa posizione, a quell’altitudine, per un’ora, la Terra si sposterà di 1 km sotto il elicottero stesso. Chiedi ai piloti: questo non succede, in nessun caso. Un’altra prova che l’esperienza di Guglielmini è falsa, che la Terra non si muove e che l’atmosfera non ruota.

---

Michele Vassallo è un ingegnere meccanico. Nel 2015, quando scoprì il movimento emergente degli American Flat Earthers, si sentì stupito e affascinato. Presto si rese conto che la Terra non poteva essere un globo. Nonostante il fatto che gli argomenti venuti alla ribalta fossero e siano ancora incompleti e contengano molti errori, il concetto generale di una terra piatta sembra assolutamente degno di indagine.

Tra le sue migliori scoperte c’è la reintroduzione dell’etere nella fisica della terra piatta e una nuova visione della natura della luce.

E’ coautore del libro “The real measures of the (flat)Earth” edito da Aracne editore e del blog “rifugiatidipella.com“. Dal 2019 produce materiale video inerente la Terra piatta sul suo canale Youtube “earthmeasured”.